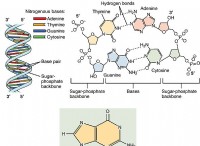
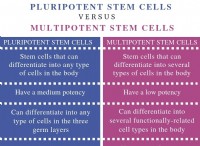
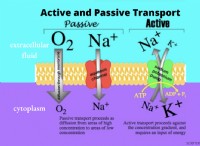
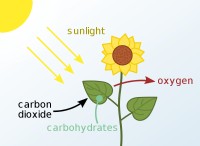
基本的な数学スキルが重要です:
* データ分析と解釈: 微生物学には、多くのデータ収集と分析が含まれます。実験を解釈し、結論を引き出すには、手段、標準偏差、仮説テストなどの基本的な統計を理解する必要があります。
* 計算: 希釈、濃度、成長率、および微生物培養および実験に関連するその他の計算で作業することになります。
* 問題解決: 微生物学は、微生物の成長、代謝、および相互作用に関連する問題を解決するために、論理的推論と定量的思考を適用することがよくあります。
微生物学に関連する数学の特定の領域:
* 統計: 実験データを分析し、結果の重要性を理解し、有効な結論を導き出すために不可欠です。
* 代数: 微生物の成長、希釈計算、およびその他の実用的なアプリケーションに関連する方程式を解くのに役立ちます。
* 基本的な計算: 人口のダイナミクスを理解し、微生物の成長をモデル化するために必要になる場合があります。
* 生物統計: 特に研究と疫学において、複雑なデータセットの分析を支援します。
準備方法:
* 数学の基礎に焦点を当てます: 必要に応じて、代数、基本統計、および基本的な計算に強力な基盤があることを確認してください。
* 問題解決の実践: 現実世界の微生物学シナリオに数学的概念を適用する練習。
* オンラインリソースを利用: 多くのオンラインリソースは、基本的な数学のための無料のチュートリアルと練習演習を提供しています。
覚えておいてください: 研究科学者になることを計画していなくても、強力な数学的スキルは、微生物学的概念を理解し、効果的に適用するために有利です。