気体の運動分子理論

気体の運動分子理論 (KMT または単に気体の動力学理論 ) は、統計力学を使用して気体の巨視的な特性を説明する理論モデルです。これらの特性には、ガスの圧力、体積、温度、およびその粘度、熱伝導率、質量拡散率が含まれます。これは基本的に理想気体の法則の適応ですが、気体の運動分子理論は、通常の条件下でのほとんどの実在気体の挙動を予測するため、実用的なアプリケーションがあります。この理論は、物理化学、熱力学、統計力学、工学で使用されます。

ガスの運動分子理論の仮定

この理論は、ガス粒子の性質と挙動について仮定しています。基本的に、これらの仮定は、気体が理想気体として振る舞うというものです:

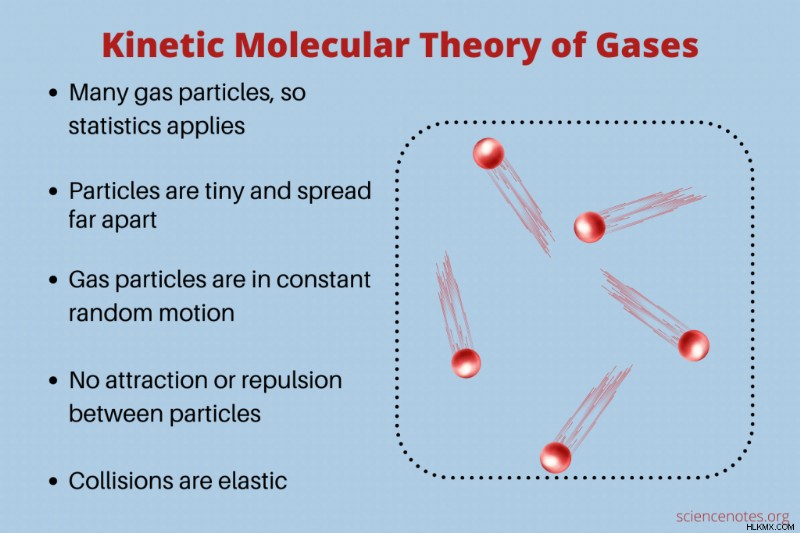
• ガスには多くの粒子が含まれているため、統計の適用は有効です。
• 各粒子の体積はごくわずかで、隣の粒子から離れています。つまり、各粒子は点質量です。ガスの体積のほとんどは空の空間です。
• 粒子は相互作用しません。つまり、互いに惹かれたり反発したりしません。
• ガス粒子は常にランダムな動きをしています。
• ガス粒子間または粒子と容器壁間の衝突は弾性的です。つまり、分子は互いにくっつかず、衝突でエネルギーが失われることはありません。

これらの仮定に基づいて、ガスは予測可能な方法で動作します:

• ガス粒子はランダムに移動しますが、常に直線的に移動します。
• ガス粒子が移動して容器に衝突するため、容器の体積はガスの体積と同じです。
• ガスの圧力は、容器の壁に衝突する粒子の数に比例します。
• 温度が上昇すると、粒子は運動エネルギーを獲得します。運動エネルギーが増加すると、衝突の数とガスの圧力が増加します。したがって、圧力は絶対温度に正比例します。
• すべての粒子が同じエネルギー (速度) を持っているわけではありませんが、非常に多くの粒子があるため、気体の温度に比例する平均運動エネルギーを持っています。
• 個々の粒子間の距離はさまざまですが、平均自由行程と呼ばれる平均距離があります。
• ガスの化学的性質は問題ではありません。したがって、酸素ガスの容器は空気の容器とまったく同じように動作します。

理想気体の法則は、気体の特性間の関係をまとめたものです:

PV =nRT

ここで、P は圧力、V は体積、n は気体のモル数、R は理想気体定数、T は絶対温度です。

気体の動力学理論に関連する気体の法則

気体の動力学理論は、さまざまな巨視的特性間の関係を確立します。特定の値を一定に保つと、理想気体の法則の特殊なケースが発生します。

• Pαn :一定の温度と体積では、圧力はガスの量に正比例します。たとえば、容器内のガスのモル数を 2 倍にすると、圧力が 2 倍になります。
• V α n (アボガドロの法則) :一定の温度と圧力では、体積は気体の量に正比例します。たとえば、気体の粒子の半分を取り除いた場合、圧力が同じままになる唯一の方法は、体積が半分に減少することです。
• P α 1/V (ボイルの法則) :気体の量と温度が変化しないと仮定すると、体積が減少すると圧力が増加します。つまり、気体は圧縮可能です。温度を変えずに圧力をかけると、分子は速く動きません。体積が減少すると、粒子は容器の壁までの距離が短くなり、容器の壁に衝突する頻度が高くなります (圧力が増加します)。体積が増えるということは、粒子がより遠くまで移動して容器の壁に到達し、衝突する頻度が減ることを意味します (圧力が減少します)。
• V α T (シャルルの法則) :一定の圧力とガスの量を仮定すると、ガスの体積は絶対温度に正比例します。つまり、温度を上げると、気体は体積が増えます。温度を下げると体積が減少します。たとえば、ガスの温度が 2 倍になると、体積が 2 倍になります。
• P α T (ゲイ-リュサックまたはアモントンの法則) :質量と体積を一定に保つと、圧力は温度に正比例します。たとえば、温度が 3 倍になると、圧力は 3 倍になります。ガスの圧力を解放すると、温度が下がります。
• v α (1/M) (グラハムの拡散の法則) :ガス粒子の平均速度は、分子量に正比例します。または、2 つのガスを比較すると、v₁ /v₂ =M₂ /M₁ .
• 運動エネルギーと速度 :平均運動エネルギー (KE) は、気体分子の平均速度 (二乗平均平方根または rms または u) に関連します:KE =1/2 μ
• 温度、モル質量、RMS :運動エネルギーの式と理想気体の法則を組み合わせると、二乗平均速度 (u) が絶対温度とモル質量に関連付けられます:u =(3RT/M)
• ダルトンの分圧の法則 :混合ガスの全圧は、構成ガスの分圧の合計に等しくなります。

問題例

ガス量を 2 倍にする

圧力が 100 kPa から始まり、ガスの量が 5 モルから 2.5 モルに変化した場合のガスの新しい圧力を求めます。温度と体積が一定であると仮定します。

重要なのは、一定の温度と体積で理想気体の法則がどうなるかを判断することです。 P α n を認識すると、モル数を半分に減らすと圧力も半分になることがわかります。したがって、新しい圧力は 100 ÷ 2 =50 kPa です。

それ以外の場合は、理想気体の法則を並べ替えて、2 つの方程式を互いに等しく設定します。

P₁ /n₁ =P₂ /n₂ (V、R、および T は変更されていないため)

100/5 =x/2.5

x =(100/5) * 2.5

x =50kPa

RMS 速度の計算

分子の速度が 3.0、4.5、8.3、および 5.2 m/s の場合、気体中の分子の平均速度と rms 速度を求めます。

値の平均または平均は、単純にそれらの合計を値の数で割ったものです:

(3.0 + 4.5 + 8.3 + 5.2)/4 =5.25 メートル/秒

ただし、二乗平均速度または rms は、速度の二乗和を値の総数で割った値の平方根です。

u =[(3.0 + 4.5 + 8.3 + 5.2)/4] =5.59 メートル/秒

温度からの RMS 速度

298 K での酸素ガスのサンプルの RMS 速度を計算します。

温度はケルビン (絶対温度) であるため、単位変換は必要ありません。ただし、酸素ガスのモル質量が必要です。酸素の原子質量からこれを取得します。 1 分子あたり 2 つの酸素原子があるため、2 を掛けます。次に、1 モルあたりのグラム数から 1 モルあたりのキログラム数に変換して、単位が理想気体定数の単位と一致するようにします。

MM =2 x 18.0 g/mol =32 g/mol =0.032 kg/mol

u =(3RT/M) =[(3)(8.3145 J/K· mol)(298 K) / (0.032 kg/mol)]

ジュールは kg・m・s であることを忘れないでください。

u =482 メートル/秒

参考文献

• チャップマン、シドニー。カウリング、トーマス・ジョージ（1970）。 不均一な気体の数学的理論:気体の粘性、熱伝導、および拡散の動力学的理論の説明 （第3版）。ロンドン:ケンブリッジ大学出版局
• グラッド、ハロルド (1949)。 「希薄化ガスの動力学理論について」。 純粋数学と応用数学に関するコミュニケーション . 2 (4):331–407。 doi:10.1002/cpa.3160020403
• Hirschfelder, J. O.;カーチス、CF。バード、RB（1964）。 気体と液体の分子理論 （改訂版）。ワイリー-インターサイエンス。 ISBN 978-0471400653.
• マクスウェル、J. C. (1867)。 「気体の力学理論について」。 ロンドン王立協会の哲学的取引 . 157:49–88. doi:10.1098/rstl.1867.0004
• ウィリアムズ、M.M.R. (1971)。 粒子輸送理論の数学的方法 .バターワース、ロンドン。 ISBN 9780408700696.