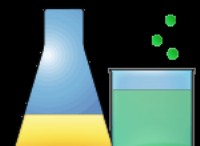
$$ hno_2 \ rightleftharpoons h^ + + no_2^ - $$
弱酸のpHは、次の式を使用して計算できます。
$$ ph =- \ log [h^+] $$
ここで、[h^+]はリットルあたりのモル(m)の水素イオン濃度です。
亜酸化酸の解離定数(ka)は、25°Cで4.5 x 10^(-4)です。 Kaは酸の強度の尺度であり、Kaが小さいほど酸が弱くなります。亜硝酸の場合:
$$ ka =[h^+] [no_2^ - ]/[hno_2] $$
xが平衡状態で生成されたh^+およびno2イオンの濃度であり、hno2の初期濃度はcであると仮定すると、次のとおりです。
$$ [h^+] =[no_2^ - ] =x $$
$$ [hno_2] =c -x $$
これらの濃度をKa式に置き換えます:
$$ 4.5 \ times 10^{ - 4} =x^2/(c -x)$$
平衡状態では、コンジュゲート塩基の濃度であるNO2-は、HNO2の初期濃度に比べて小さいため、分母のC≈[hno2]と仮定できます。したがって、方程式を簡素化すると、次のことがあります。
$$ x^2 +(4.5 \ times 10^{-4})x-(4.5 \ times 10^{-4})c =0 $$
Xを解く、水素イオン濃度:
$$ x =\ frac {-b±√(b^2-4ac)} {2a} $$
ここで、a =1、b =4.5 x 10^( - 4)、およびc =- (4.5 x 10^( - 4))c。
水素イオン濃度の計算(x):
$$ x =\ frac { - (4.5 \ times 10^{ - 4})±√((4.5 \ times 10^{-4})^2-4(1)(-4.5 \ times 10^{ - 4})c)} {2(1)} $$
$$ x =\ frac {4.5 \ times 10^{-4}±0.0198c} {2} $$
水素イオン濃度は陰性ではないため、正の根を取得します。
$$ x =\ frac {0.0198c + 4.5 \ times 10^{-4}} {2} $$
Ka式を方程式に置き換える:
$$ x =\ frac {ka [hno_2] + ka} {2} $$
$$ x =\ frac {(4.5 \ times 10^{-4})[hno_2] + 4.5 \ times 10^{-4}} {2} $$
25°Cで:
$$ ph =- \ log \ left(\ frac {(4.5 \ times 10^{-4})[hno_2] + 4.5 \ times 10^{-4}} {2} \ right)$$
例えば:
[hno2] =0.1 mの場合:
$$ ph =- \ log \ left(\ frac {(4.5 \ times 10^{ - 4})(0.1) + 4.5 \ times 10^{ - 4}} {2} \ right)=2.85 $$
したがって、0.1 m亜硝酸溶液のpHは約2.85です。