関数の導関数は、その関数の特定の点における初期関数の変化率を示す関数です。関数の導関数は、初期関数の出力が入力のわずかな変化にどの程度敏感であるかの尺度と考えることができます。導関数は、任意の時点で関数がどれだけ速く変化しているかを示します。そのため、導関数は、変位、速度、加速度などの変化率を含む状況をモデル化するのに役立ちます。
関数の導関数:
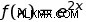
e の形式で関数の導関数を見つけるための特別な規則によって決定できます。 一般的なルールは次のとおりです。
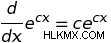
したがって、このルールを使用すると、次のことを判断できます。
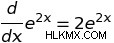
つまり、関数ƒ(x) =eの導関数 ƒ'(x) =2e .この導関数は、入力の変化に対する元の関数の出力の変化率を示します。基本的に、2 つの方程式は、関数の出力ƒ(x) =e を示しています。 2e 倍に増加 入力ごと。したがって、x の値が 1 の場合、その値を方程式に代入すると、次のようになります。
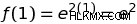
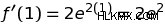
これらの方程式から 2 つのことがわかります。まず、点 x=1 で、関数 ƒ(x) の出力は e になります。 .第二に、導関数は、点 x=1 で、ƒ(x) の出力が 2e の係数で変化していることを示しています。 .
デリバティブとは?
前述のように、関数の導関数は、関数の出力がその入力の変化に対してどの程度敏感であるかの尺度です。 ƒ(x) の導関数は、x の変化に対する ƒ(x) の出力の変化率を測定します。
線形方程式yがある単純なケースを想像してみてください =2x+3。さらに、(1,5) と (2,7) の直線上にある x y 座標の 2 つのセットを選択します。これら 2 点間の x に関する関数の変化率は?これは次の計算で計算できます:
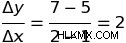
これは、これらの 2 点間で、関数の出力が 2 倍変化していることを意味します。この値 2 は、線形方程式 y の傾きにも等しいことに注意してください。 =2x +3.
実際、方程式上の任意の 2 点について y =2x+3、変化率は常に 2 です。これは、関数のすべての点で、関数の出力が x に対して 2 倍に増加していることを意味します。ちなみに、これは導関数を見つけるための最初のルールです:ƒ(x) が線形関数の場合 y= mx+ b :
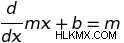
つまり、y= の形式の任意の線形関数に対して mx+ b 、その関数の導関数は傾きに等しい m . x の変化に対する y の変化率を表す線形方程式について考えてみると、関数の傾き m 入力ごとに、出力の変化率が 2 倍に変化するため、その変化率が得られます。
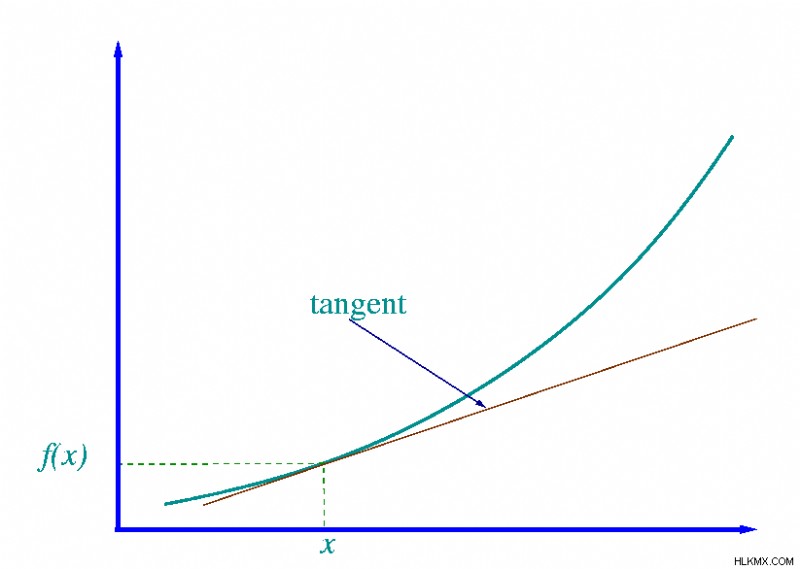
高次関数(x、xなど)の導関数を見つけるプロセスは、2点間の勾配を見つけるこのプロセスを一般化し、Δxが任意に小さくなるにつれて比Δy/Δxが近づく限界値を見つけます。その結果、ある点での関数の導関数は、本質的に単一点でのグラフの傾きを示します。これは、ある点での関数の導関数が、その点でのグラフに接する直線の傾きを与えるという事実にも見られます.
わかりました。これで問題ありませんが、各時点で ƒ(x)=x のような関数の変化率を見つけるにはどうすればよいでしょうか? y のような方程式とは異なります =mx +b、 関数ƒ(x)=xの変化率 は一定ではなく、あらゆる点で変化しています。この種の累乗関数の変化率をどのように捉えますか?
線形方程式の場合、y の変化に対する x の変化の比率 (Δy/Δx) を求めることで、方程式の変化率を求めたことを思い出してください。関数ƒ(x)=xから始めましょう . x の 2 つの値を選択すると、ƒ(1)=1 と ƒ(2) =4 が得られます。Δy/Δx を解くと、(4-1)/(2-1)=4 が得られます。これらの 2 点間を通る直線の傾きは 4 です。ここで、このプロセスを繰り返したとします。互いに非常に近い x 値、たとえば 1 と 1.5 を選択します。これにより、以下が得られます。
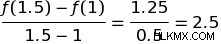
もっと近づいてみたら? 1と1.1はどうですか?これらの値を差し込むと、次のようになります。
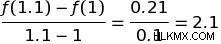
1 と 1.01 はどうですか?:これらは次のことを示しています:
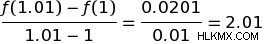
Δx が任意に小さくなると、Δy/Δx の比率が何らかの値(この場合は 2)に近づくことに注意してください。グラフで言えば、これは、x の差をどんどん小さくしていくほど、傾きがより近くなることを意味します。一点で関数の。これにより、最終的にその時点での関数の微分が得られます。これは 2 です。
これで、関数の導関数を 1 点で近似する方法がわかりました。関数の導関数は、点に近づく一連のより小さい Δx によって近似できます。これにより、極限表記で書かれた値の導関数を与えるための一般的な定義が得られます。つまり:
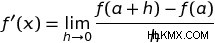
基本的に、この方程式は、f(a) の導関数が、h が無限に小さくなるにつれて比 Δy/Δx が近づく限界に等しいことを示しています。 h の値 これが 0 に非常に近い場合、その時点でのグラフの傾きの適切な近似値が得られます。 h の値を小さくするほど、関数のその点での接線の傾きに近づくという考え方です。これは導関数の正式な定義であり、導関数を導出するために使用できます 関数 —つまりある時点ですべての入力値を初期関数の変化率にマッピングする関数。
関数 ƒ(x)=x2 に戻りましょう .この関数を導関数の定義に組み込むと、ƒ(x)=x2 の導関数を導出できるはずです。 .そうすることで、以下が得られます:
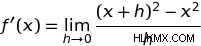
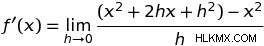
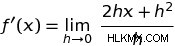
h を因数分解すると、次のようになります。

この方程式では、h は非常に小さな値であると想定されているため、本質的に方程式内の h を無視して次のように単純化できます。
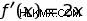
つまり、ƒ(x) =x の微分関数はちょうど ƒ'(x) =2x です。任意の点 x での関数 x の変化率は 2x に等しい。したがって、x=1 では ƒ'(1)=2、x=2 では ƒ'(2)=4、x=3 では ƒ'(3)=6 などとなります。微分関数は、入力値の変化に対する各点での初期関数の変化率を示します。このグラフの x 値ごとに、関数は 2x に比例する割合で変化しています。
導関数計算の一般規則
最初の規則は、定数関数の導関数を含みます。一定の出力を与える関数の場合、その関数の導関数は 0 です。これは次のとおりです:
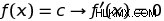
定数関数は同じ出力しか与えないため、変化しないため、その変化率は常に 0 です。したがって、ƒ(x)=7 の場合、ƒ'(x)=0 です。
次に、x の導関数を任意の n 次多項式に導出する前のプロセスを一般化すると、多項式項の導関数を見つけるための一般的なルールが得られます。
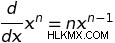
これは パワー ルール と呼ばれます 多次多項式の導関数を計算するために使用できます。べき乗則を使用して、x の導関数は 3x、x の導関数は 4x などと判断できます。
指数関数の場合、関数自体に底の自然対数を掛けることで導関数を見つけることができます。これは:
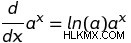
これは指数規則と呼ばれます .指数規則は、e の導関数を見つけるための特別な規則のより一般化されたバージョンです。 すべての関数のうち、f(x)=e 導関数がそれ自体である唯一の関数です。つまり、グラフに接するすべての直線の傾き e e. です。

上記の 4 つの式は、式の導関数を見つけるための最も一般的な規則です。さらに、関数とその導関数の組み合わせを管理する規則があります。たとえば、和の法則があります つまり:
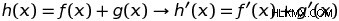
和の規則は、ある関数 h が他の 2 つの関数 f と g の和である場合、h の導関数は f と g の導関数の和に等しいことを示しています。和の法則により、多項式の各項の導関数を見つけ、それらを足し合わせて全導関数を得ることができます。たとえば、ƒ(x)=x+4x-3x を想像してみてください。和の法則は、この関数の導関数がその構成関数の導関数の和に等しいことを示しているため、ƒ'(x)=3x+8x-3
次は製品ルールです 、関数の積の導関数を見つけるための式を与えます。製品ルールは次のとおりです:

積則は、2 つの関数の積の導関数が、最初の関数に 2 番目の関数の導関数を掛けたものに、2 番目の関数に最初の関数の導関数を掛けたものに等しいことを示しています。したがって、ƒ(x)=sin(x)x の導関数は、ƒ'(x)=sin(x)2x + xcos(x) になります。この積規則の順序は、ニーモニック「左ディー右、右ディー左」 (LDR RDL) で覚えることができます。
最後はチェーンルール 、関数の構成の導関数を記述します。ある関数が他の 2 つの関数の合成である場合、連鎖則により、合成関数の導関数は、g(x) で評価された最初の関数の導関数に g(x) の導関数を掛けたものに等しいことがわかります。象徴的には:
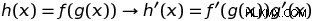
連鎖律により、関数を関数内に置くことができ、その複合関数の導関数を得ることができます。
これらの規則を使用して、ほとんどの標準的な多項式の導関数を計算できます。一部の関数はより複雑ですが、上記のルールを確実に適用することで、実数値関数のレイヤーを剥がして導関数を導き出すことができます。