位置エネルギーは、その位置によってオブジェクトに起因するエネルギーです。位置が変わると、総エネルギーは変わりませんが、位置エネルギーの一部が運動エネルギーに変換されます。摩擦のないジェット コースターは、古典的なポテンシャルと運動エネルギーの例題です。
ジェット コースターの問題は、エネルギー保存を使用して、高さの異なる摩擦のないトラック上の速度または位置、またはカートを見つける方法を示しています。カートの総エネルギーは、その重力位置エネルギーと運動エネルギーの合計として表されます。この総エネルギーは、トラックの長さ全体で一定のままです。
位置エネルギーと運動エネルギーの例の問題
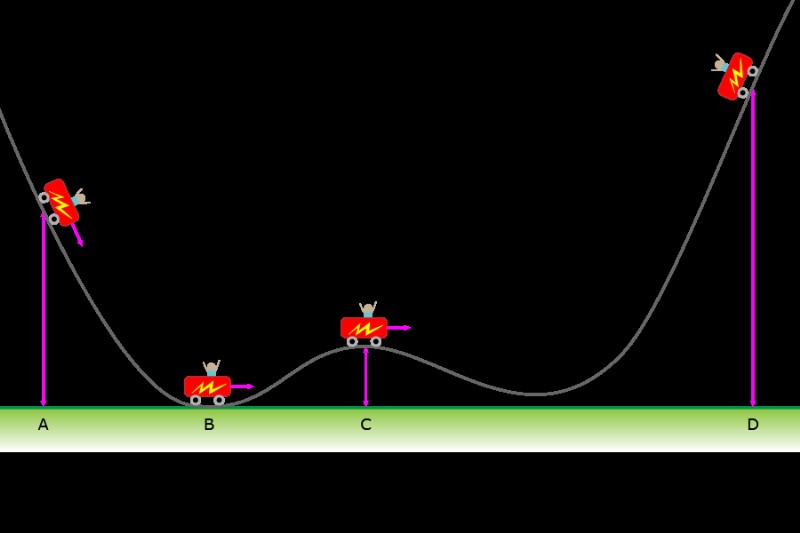
質問:
カートは摩擦のないジェット コースター トラックに沿って移動します。点 A では、カートは地上 10 m で、2 m/s で移動します。
A) カートが地面に着くときの点 B での速度は?
B) カートが 3 m の高さに達したときの点 C でのカートの速度は?
C) カートが停止する前に到達できる最大の高さは?
解決策:
カートの総エネルギーは、位置エネルギーと運動エネルギーの合計で表されます。
重力場における物体のポテンシャル エネルギーは、次の式で表されます
PE =mgh
どこ
PEは位置エネルギーです
m は物体の質量
g は重力による加速度 =9.8 m/s
h は測定面からの高さです。
運動エネルギーは、運動中の物体のエネルギーです。という式で表されます
KE =½mv
どこ
KE は運動エネルギー
m は物体の質量
v はオブジェクトの速度です。
システムの総エネルギーは、システムのどの点でも保存されます。全エネルギーは、位置エネルギーと運動エネルギーの合計です。
合計 E =KE + PE
速度または位置を見つけるには、この全エネルギーを見つける必要があります。点 A では、カートの速度と位置の両方がわかっています。
合計 E =KE + PE
合計 E =½mv + mgh
合計 E =½m(2 m/s) + m(9.8 m/s)(10 m)
合計 E =½m(4 m/s) + m(98 m/s)
合計 E =m(2 m/s) + m(98 m/s)
合計 E =m(100 m/s)
質量の値は今のところ表示されたままにしておきます。各パートを完了すると、この変数がどうなるかがわかります。
パート A:
カートは点 B の地面の高さにあるので、h =0 m.
合計 E =½mv + mgh
合計 E =½mv + mg(0 m)
合計 E =½mv
この時点でのエネルギーはすべて運動エネルギーです。全エネルギーは保存されるので、点 B の全エネルギーは点 A の全エネルギーと同じです。
A での総 E =B での総エネルギー
m(100 m/s) =½mv
両辺をmで割る
100 m/s =½v
両辺を 2 倍する
200 メートル/秒 =v
v =14.1 m/s
ポイント B での速度は 14.1 m/s です。
パート B:
点 C では、h (h =3 m) の値しかわかりません。
合計 E =½mv + mgh
合計 E =½mv + mg(3 m)
前と同じように、全エネルギーは保存されます。 A での総エネルギー =C での総エネルギー。
m(100m/s) =½mv + m(9.8m/s)(3m)
m(100 m/s) =½mv + m(29.4 m/s)
両辺を m で割る
100m/s =½v + 29.4m/s
½v =(100 – 29.4) m/s
½v =70.6 m/秒
v =141.2 メートル/秒
v =11.9 メートル/秒
点 C での速度は 11.9 m/s です。
パート C:
カートが停止するか、v =0 m/s になると、カートは最大の高さに達します。
合計 E =½mv + mgh
合計 E =½m(0 m/s) + mgh
合計 E =mgh
総エネルギーは保存されるので、点 A の総エネルギーは点 D の総エネルギーと同じです。
m(100 m/s) =mgh
両辺を m で割る
100 メートル/秒 =gh
100 メートル/秒 =(9.8 メートル/秒) h
h =10.2 m
カートの最大高さは 10.2 m です。
答え:
A) 地上でのカートの速度は 14.1 m/s です。
B) 3 m の高さでのカートの速度は 11.9 m/s です。
C) カートの最大高さは 10.2 m です。
このタイプの問題には、重要なポイントが 1 つあります。それは、システムのすべての点で総エネルギーが保存されるということです。ある点での総エネルギーがわかれば、すべての点での総エネルギーがわかります。