位置エネルギーと運動エネルギーは、エネルギーの 2 つの主要なタイプです。ここでは、定義、例、単位、式、計算方法など、運動エネルギーについて説明します。
運動エネルギーの定義
物理学では、運動エネルギーは、その運動のために物体が持つエネルギーです。これは、特定の質量の物体を静止状態から特定の速度まで加速するのに必要な仕事として定義されます。質量が速度に達すると、速度が変化しない限り、その運動エネルギーは変化しません。ただし、速度、つまり運動エネルギーは基準フレームに依存します。つまり、物体の運動エネルギーは不変ではありません。
運動エネルギー単位
運動エネルギーの SI 単位はジュール (J) で、kg・m・s です。運動エネルギーの英国単位はフィート ポンド (ft⋅lb) です。運動エネルギーはスカラー量です。大きさはありますが、方向はありません。
運動エネルギーの例
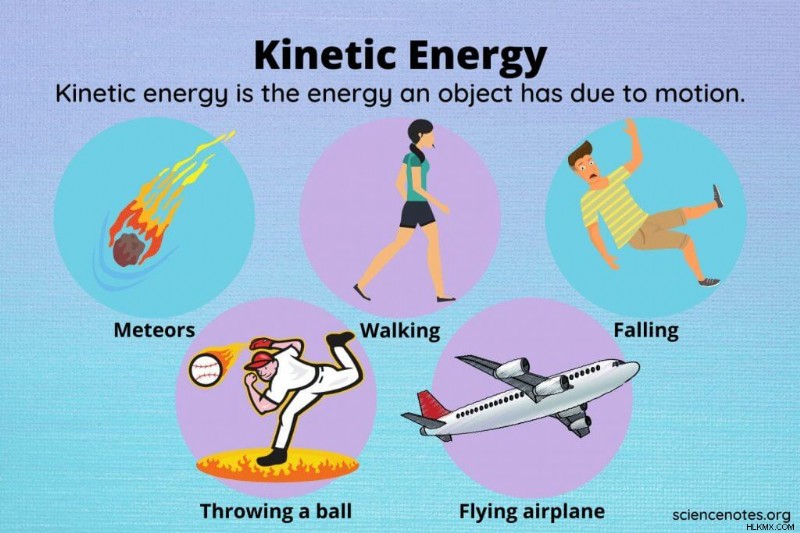
質量 (または見かけの質量) と運動があると考えられるものはすべて、運動エネルギーの例です。運動エネルギーの例:
- 空飛ぶ飛行機、鳥、またはスーパーヒーロー
- ウォーキング、ジョギング、サイクリング、水泳、ダンス、ランニング
- 落下または物を落とす
- ボールを投げる
- 車の運転
- ヨーヨーで遊ぶ
- ロケットの打ち上げ
- 回る風車
- 空を横切る雲
- 風
- 雪崩
- 滝または流れる小川
- 電線に流れる電気
- 周回衛星
- 地球に落ちてくる隕石
- スピーカーから耳に伝わる音
- 原子核を周回する電子
- 太陽から地球に移動する光 (光子には運動量があるため、見かけの質量があります)
運動エネルギー式
運動エネルギー (KE) の式は、エネルギーを質量 (m) と速度 (v) に関連付けます。
KE =1/2 mv
質量は常に正の値であり、任意の値の 2 乗は正の数であるため、運動エネルギーは常に正です。また、これは、運動の方向に関係なく、速度が最大のときに最大の運動エネルギーが発生することを意味します。
運動エネルギー方程式から、物体の速度は質量よりも重要であることがわかります。そのため、小さな物体でも、すばやく動いている場合は多くの運動エネルギーを持っています。
運動エネルギーの式は古典物理学で機能しますが、速度が光速 (c ).
運動エネルギーの計算方法
運動エネルギーの問題を解決する鍵は、1 ジュールが 1 kg・m・s に等しいことを覚えておくことです。速度は速度の大きさなので、運動エネルギー方程式で使用できます。それ以外の場合は、単位を分数で見てください。たとえば、(1)/(400 m/s) は (1/400) s/m と同じです。
例 #1
1.4 m/s の速度で移動する 68 kg の人の運動エネルギー (つまり、典型的な人の歩行の運動エネルギー) を計算します。
KE =1/2 mv
数字を入れる:
KE =1/2(68kg)(1.4m/s)
KE =66.64kg・m・s
KE =66.64 J
例 #2
1000 J の運動エネルギーで 20 m/s で移動する物体の質量を計算します。
運動エネルギー方程式を並べ替えて、質量を求めます:
m =2KE/v
m =(2)(1000kg・m・s)/(20m/s)
m=(2000kg・m・s)/(400m/s)
m =5kg
運動エネルギーと位置エネルギーの違い
運動エネルギーは位置エネルギーに変換でき、その逆も可能です。運動エネルギーは物体の動きに関連するエネルギーであり、位置エネルギーは物体の位置によるエネルギーです。他のすべての種類のエネルギー (電気エネルギー、化学エネルギー、熱エネルギー、核エネルギーなど) には、運動エネルギー、位置エネルギー、またはその 2 つの組み合わせがあります。システムの運動エネルギーと位置エネルギーの合計 (その総エネルギー) は、エネルギー保存則により一定です。量子力学では、運動エネルギーとポテンシャル エネルギーの和をハミルトニアンと呼びます。
摩擦のないジェット コースターは、運動エネルギーとポテンシャル エネルギーの相互作用の良い例です。トラックの最上部では、ジェット コースターの位置エネルギーは最大になりますが、運動エネルギーは最小 (ゼロ) になります。カートがトラックを下るにつれて、速度が上がります。トラックの最下部では、位置エネルギーが最小 (ゼロ) になり、運動エネルギーが最大になります。
参考文献
- Goel, V. K. (2007). 物理学の基礎 .タタ・マグロウヒル教育. ISBN 978-0-07-062060-5.
- サーウェイ、レイモンド A.; Jewett、ジョン W. (2004)。 科学者とエンジニアのための物理学 (第6版)。ブルックス/コール。 ISBN 0-534-40842-7.
- ティプラー、ポール。ルウェリン、ラルフ(2002)。 現代物理学 (第4版)。 W・H・フリーマン。 ISBN 0-7167-4345-0.







