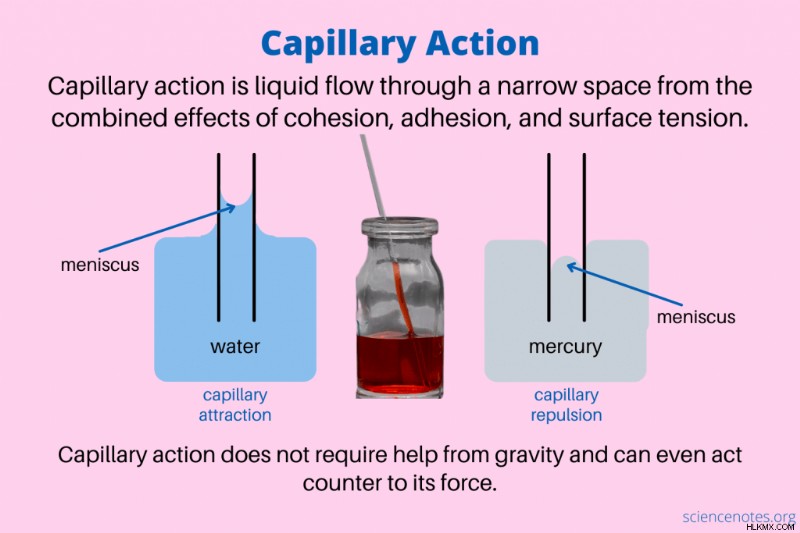
毛管作用 表面張力、凝集力、粘着力による狭いチューブまたは空間を通る流体の流れです。たとえば、細いチューブを水の中に入れると、水がチューブを上っていきます。この現象の他の名前は、毛細管現象、毛細管運動、ウィッキングです。毛細管現象は重力を必要としません。実際、液体はしばしば重力に逆らって細い管の中を上昇します。
毛管作用の力 – 仕組み
毛細管現象に大きく関与する 3 つの力は、表面張力、凝集力、接着力です。
- 凝集は、液体分子が互いにくっつくときに発生します。水分子の場合、分子間の水素結合により凝集力が高くなります。
- 接着力は、液体分子が表面にどの程度付着するかを表します。水分子はガラスやプラスチックの表面にくっつきます。対照的に、水銀原子は互いにくっつきますが、容器の表面にはあまり引き付けられません.
- 表面張力は、液体の表面積を最小化する、空気との界面における液体の張力です。水と水銀はどちらも高い表面張力を持っています。細いチューブでは、これらの 2 つの液体によって形成されるメニスカスが湾曲しています。ただし、水は容器の壁に向かって曲がりますが、水銀は毛細血管の中心で丸い形を形成します。
- 重力は、垂直チューブ内の液体を下向きに引っ張るため、毛細管内で液体が上昇する距離に影響します。
多くの液体は水のように振る舞い、毛細管の中を上昇します。ただし、水銀のような液体は、チューブを取り囲む液体よりも低いレベルまで上昇します。
凸状のメニスカスは、分子が容器よりも互いに引き付けられる場合に形成されます。たとえば、水銀はガラスに凸状のメニスカスを形成します。凹状メニスカスは、分子が互いによりも容器に引き付けられる場合に形成されます。たとえば、水はガラスに凹状のメニスカスを形成します。メニスカスの形状は、液体の組成と容器の組成の両方に依存します。たとえば、プラスチックの水のメニスカスはほぼ平らです。
毛細管現象の例
日常生活における毛細管現象には、おなじみの例がたくさんあります:
- 水の入ったグラスにストローを入れると、ストロー内の液面がグラス内の水の高さよりも高くなります。
- 毛細管現象により、コンクリートと乾式壁の湿気が上昇します。
- 目の涙管 (涙管) は、目の表面から継続的に涙を排出します。
- ろうそくの芯は、ろうそくの炎を絶えず供給する液体ワックスを吸収します。ペイント ブラシとランプの芯は、同じように液体を吸収します。
- ペーパー タオルは毛細管現象を利用して水を吸い上げます。
- 汗を逃がす生地は、毛細管現象も利用しています。
植物の茎や幹を上る水の移動 (蒸散) には毛細管現象が関与しますが、葉からの蒸発と根からの浸透圧にも依存しています。
毛管作用の用途
毛細管現象にはいくつかの用途があります。例:
- 万年筆は毛細管現象を利用してインクを吸い上げます
- 薄層クロマトグラフィーとペーパー クロマトグラフィーは毛細管現象を利用します。
- キャピラリー チューブは、血液などの少量のサンプルを採取する、科学および医学における細いチューブです。

キャンディ クロマトグラフィー プロジェクト
カラフルなキャンディーの色素を分離する楽しいペーパー クロマトグラフィー プロジェクトに毛細管現象を適用します。
メニスカスの高さの式
キャピラリー チューブ、試験管、またはビュレットのメニスカス ラインで液面を測定してください。毛細管現象を説明する液柱のメニスカスの高さを計算する式があります:
h =2γcosθ / ρgr
ここ:
- h は液柱のメニスカスの高さです
- γ は液体空気環境における表面張力です
- θ は、液体とカラム壁の間の接触角です
- ρ は液体の密度です
- g は重力による加速度
- r はチューブの内径です
この式を使用して、チューブの半径の影響に注意してください。チューブが細いほど、半径が小さくなり、毛細管現象によって液体が遠くまで移動します。
液体輸送量の計算式
ペーパー タオルなどの乾燥した多孔質媒体は、液体を吸収する速度が時間の経過とともに遅くなります。経時的に吸収される量を計算する式があります:
V =SA√t
ここ:
- V は液体の体積
- S は吸着性または毛細管現象による媒体の吸収能力です
- A はウェット エリアの断面です
液体の吸収率は、温度、透過性、湿度など、いくつかの要因によって異なります。
参考文献
- バチェラー、G.K. (1967)。 流体力学入門 .ケンブリッジ大学出版局。 ISBN 0-521-66396-2.
- de Gennes, Pierre-Gilles; Brochard-Wyart、フランソワーズ。ケレ、デビッド(2004)。 毛管現象と湿潤現象 .スプリンガー ニューヨーク。 ISBN 978-1-4419-1833-8。 doi:10.1007/978-0-387-21656-0
- フリーマン、スコット (2014)。 生物科学 .アメリカ合衆国:ピアソン。 ISBN 978-0-321-74367-1.
- リュー、M.;ら。 (2016)。 「蒸発は、多孔質媒体における半径方向の毛管貫通を制限する」。 ラングミュア . 32 (38):9899–9904. doi:10.1021/acs.langmuir.6b02404