ジュネーブのラージ ハドロン コライダーでは、物理学者が陽子を 17 マイルのトラックの周りに発射し、ほぼ光速で衝突させます。これは世界で最も精巧に調整された科学実験の 1 つですが、量子デブリを理解しようとするとき、物理学者はファインマン図と呼ばれる驚くほど単純なツールから始めます。これは、子供が状況を描写する方法とそれほど変わらないものです。
ファインマン図は、1940 年代にリチャード ファインマンによって考案されました。それらは、頂点 (衝突を表す) に収束し、そこから発散して衝突から出現する破片を表す素粒子を表す線を特徴としています。それらの線は、単独で発散するか、再び収束します。衝突の連鎖は、物理学者が考える限り長くなる可能性があります。
その概略図に、関係する粒子の質量、運動量、および方向の数値を物理学者が追加します。それから彼らは骨の折れる会計手続きを開始します—これらを統合し、それを追加し、これを二乗します。最終的な結果は、ファインマン確率と呼ばれる単一の数値であり、粒子の衝突がスケッチどおりに発生する可能性を定量化します。
カリフォルニア工科大学の理論物理学者で数学者でもあるセルゲイ・グコフは、次のように述べています。
ファインマン ダイアグラムは長年にわたって物理学に役立ってきましたが、限界があります。 1つは厳密に手続き型です。物理学者は、より高い測定精度を必要とする高エネルギー粒子衝突をますます追求しています。精度が上がるにつれて、予測を生成するために計算する必要があるファインマン図の複雑さも増します。
2 番目の制限は、より基本的な性質のものです。ファインマン ダイアグラムは、物理学者が説明する潜在的な衝突と部分衝突が多いほど、数値予測がより正確になるという仮定に基づいています。摂動展開として知られるこの計算プロセスは、弱い電磁力が支配する電子の粒子衝突に対して非常にうまく機能します。陽子同士の衝突など、強い核力が支配する高エネルギー衝突ではうまく機能しません。このような場合、さらに精巧なファインマン図を描くことによって、より広い範囲の衝突を説明すると、物理学者は実際に道に迷う可能性があります。
オックスフォード大学の数学者であるフランシス・ブラウンは、「ある時点でそれが現実世界の物理学から逸脱し始めるという事実を知っています。 「知られていないのは、どの時点で図の計算をやめるべきかを推定する方法です。」
それでも、楽観的な理由があります。過去 10 年間、物理学者と数学者は、由緒あるファインマン ダイアグラムに新しい命を吹き込み、両方の分野で広範囲にわたる洞察を生み出す可能性のある驚くべき対応を探求してきました。これは、ファインマン ダイアグラムから計算された値が、代数幾何学として知られる数学の分野で発生する最も重要な数の一部と正確に一致するように見えるという奇妙な事実と関係があります。これらの値は「動機の期間」と呼ばれ、両方の設定で同じ数字が表示される明確な理由はありません。実際、1 カップの米を量るたびに、穀物の数が素数であることが観察されるのと同じくらい奇妙です。
ベルリンのフンボルト大学の物理学者である Dirk Kreimer は、次のように述べています。
現在、数学者と物理学者が協力して偶然の一致を解明しようとしています。数学者にとって、物理学は彼らが理解したい特別な種類の数に注意を喚起しています:物理学で発生するこれらの期間には隠された構造がありますか?この数のクラスにはどのような特別な性質があるでしょうか?物理学者にとって、そのような数学的理解の報酬は、乱雑な量子世界でイベントがどのように展開するかを予測する際に、新たな程度の先見の明となるでしょう.
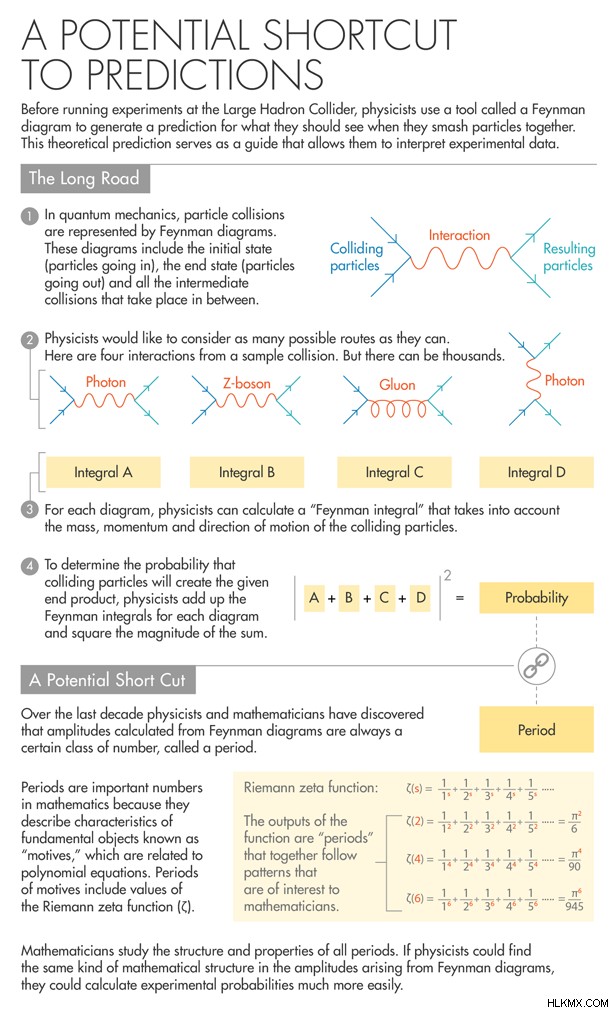
繰り返されるテーマ
今日、周期は数学の最も抽象的な主題の 1 つですが、より具体的な関心事として始まりました。 17 世紀初頭、ガリレオ ガリレイなどの科学者は、振り子が 1 回転するのにかかる時間を計算する方法に関心を持っていました。彼らは、計算が、振り子の長さと解放角度に関する情報を組み合わせた関数の積分 (一種の無限和) を取ることに要約されることに気付きました。同じ頃、ヨハネス・ケプラーは同様の計算を使用して、惑星が太陽の周りを移動するのにかかる時間を確立しました。彼らはこれらの測定値を「期間」と呼び、運動に関して行うことができる最も重要な測定値の 1 つとして確立しました。
18 世紀から 19 世紀にかけて、数学者は周期を一般的に研究することに関心を持つようになりました。周期が振り子や惑星に関連しているだけでなく、x のような多項式関数を統合することによって生成される数のクラスとしてです。 + 2x – 6 と 3x – 4x – 2x + 6. 1世紀以上にわたり、カール・フリードリッヒ・ガウスやレオンハルト・オイラーなどの著名人が時代の宇宙を探求し、そこには根底にある秩序を示す多くの特徴が含まれていることを発見しました。ある意味では、多項式方程式の幾何学的形式を研究する代数幾何学の分野は、その隠れた構造を追求する手段として 20 世紀に発展しました。
この取り組みは 1960 年代に急速に進みました。その時までに、数学者はしばしば行うことを行っていました:彼らは、方程式のような比較的具体的なオブジェクトをより抽象的なオブジェクトに変換し、最初は明らかではなかった関係を識別できるようにすることを望んでいました.
このプロセスでは、まず、関数自体を見るのではなく、多項式関数のクラスの解によって定義される幾何学的オブジェクト (代数多様体として知られる) を見る必要がありました。次に、数学者はこれらの幾何学的オブジェクトの基本的な特性を理解しようとしました。それを行うために、彼らはコホモロジー理論として知られるものを開発しました — オブジェクトを生成するために使用された特定の多項式に関係なく、同じ幾何学的オブジェクトの構造的側面を識別する方法.
1960 年代までに、特異コホモロジー、ド ラム コホモロジー、エタール コホモロジーなど、コホモロジー理論は気を散らすところまで増殖しました。代数多様体の最も重要な特徴について、誰もが異なる見方をしているように見えた.
2014 年に亡くなった先駆的な数学者アレクサンダー・グロタンディークが、すべてのコホモロジー理論は同じものの異なるバージョンであることに気付いたのは、この雑然とした風景の中でした。
「グロタンディークが観察したことは、代数多様体の場合、これらの異なるコホモロジー理論をどのように計算しても、常に何らかの形で同じ答えを見つけるということです」とブラウンは言いました.
その同じ答え — これらすべてのコホモロジー理論の中心にあるユニークなもの — は、グロタンディークが「動機」と呼んだものでした。 「音楽では、繰り返されるテーマを意味します。グロタンディークにとって、動機はさまざまな形で何度も何度もやってくるものでしたが、それは本当に同じです」と、パリ郊外の高等科学研究所の数学者であり、グロタンディークの元同僚であるピエール・カルティエは言いました.
素因数がより大きな数の要素部分であるのと同じように、動機はある意味で多項式の基本的な構成要素です。動機には、それらに関連付けられた独自のデータもあります。物質を要素に分割し、各要素の特性 (原子番号や原子量など) を指定できるように、数学者は重要な測定値を動機に帰します。これらの測定値の中で最も重要なのは、動機の期間です。また、ある多項式方程式系で発生する動機の周期が、別の系で発生する動機の周期と同じである場合、動機が同じであることがわかります。
「特定の数である期間がわかれば、それは動機そのものを知ることとほとんど同じです」と、オックスフォード大学の数学者 Minhyong Kim は言いました。
同じ周期が予期しない状況でどのように表示されるかを確認する直接的な方法の 1 つは、「周期を取得する最も有名な例」である pi を使用することです。円周率は、1 次元の円を定義する関数の積分、2 次元の円を定義する関数の積分、球を定義する関数の積分など、さまざまな形で幾何学に現れます。この同じ値が、このように一見異なるように見える積分で繰り返されることは、古代の思想家にとっておそらく不可解でした。 「現代の説明では、球と中実の円は同じ動機を持っているため、本質的に同じ期間を持たなければならないということです」と Brown は電子メールに書いています。
ファインマンの困難な道
昔、好奇心旺盛な人々が、なぜ円周率や球体の計算で pi のような値が現れるのかを知りたがっていたとしたら、今日の数学者や物理学者は、これらの値が別の種類の幾何学的オブジェクトから生じる理由を知りたがっています:ファインマン図.
ファインマン ダイアグラムには、基本的な幾何学的側面があり、線分、光線、および頂点から形成されます。それらがどのように構築され、なぜ物理学で役立つのかを理解するために、電子と陽電子が衝突してミュー粒子と反ミュー粒子を生成する単純な実験装置を想像してみてください。その結果が起こる確率を計算するには、物理学者は入ってくる各粒子の質量と運動量、および粒子がたどった経路について何かを知る必要があります。量子力学では、粒子がたどる経路は、可能なすべての経路の平均と考えることができます。そのパスの計算は、ファインマン パス積分として知られている、すべてのパスのセットに対する積分の問題になります。
粒子の衝突が最初から最後までたどる可能性のあるすべてのルートは、ファインマン図で表すことができ、各図には独自の関連する積分があります。 (ダイアグラムとその積分はまったく同じです。) 特定の一連の開始条件から特定の結果が得られる確率を計算するには、何が起こるかを説明できるすべての可能なダイアグラムを検討し、それぞれの積分を取り、それらの積分を足し合わせます。その数値がダイアグラムの振幅です。物理学者は、この数値の大きさを 2 乗して確率を求めます。
この手順は、電子と陽電子が入り、ミュー粒子と反ミュー粒子が出てくる場合に実行するのは簡単です。しかし、それは退屈な物理学です。物理学者が本当に関心を持っている実験には、ループを含むファインマン ダイアグラムが含まれます。ループは、パーティクルが放出され、追加のパーティクルが再吸収される状況を表します。電子が陽電子と衝突すると、最終的なミューオンと反ミューオンのペアが出現する前に、無数の中間衝突が発生する可能性があります。これらの中間衝突では、光子のような新しい粒子が生成され、観測される前に消滅します。粒子の出入りは前に説明したものと同じですが、これらの観測不可能な衝突が発生するという事実は、結果に微妙な影響を与える可能性があります.
「ティンカートイズみたい。図を描くと、理論のルールに従ってさらに多くの線を接続できます」と、カリフォルニア大学リバーサイド校の物理学者である Flip Tanedo は述べています。 「より多くのスティック、より多くのノードを接続して、より複雑にすることができます。」
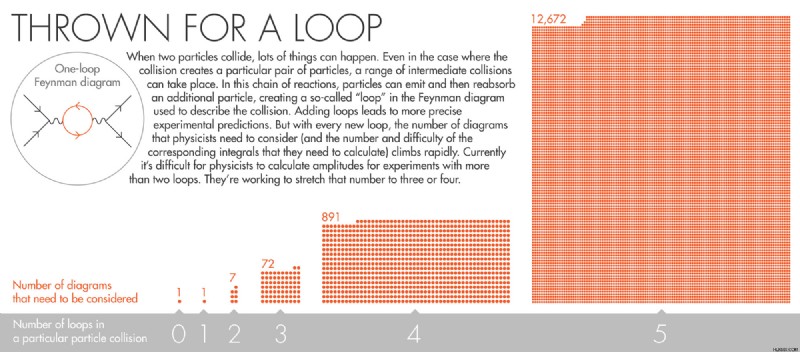
ループを考慮することにより、物理学者は実験の精度を高めます。 (ループを追加することは、より多くの有効桁数で値を計算するようなものです)。しかし、ループを追加するたびに、考慮する必要のあるファインマン図の数と、対応する積分の難しさが劇的に増加します。たとえば、単純なシステムの 1 ループ バージョンでは、ダイアグラムが 1 つだけ必要な場合があります。同じシステムの 2 ループ バージョンには、7 つのダイアグラムが必要です。 3 つのループには 72 個のダイアグラムが必要です。それを 5 ループに増やすと、計算には約 12,000 の積分が必要になります。これは、解決するのに文字通り何年もかかる計算負荷です。
数学者が周期を動機に関連付けることができるのと同じように、物理学者は、非常に多くの面倒な積分を行うよりも、与えられたファインマン ダイアグラムの構造を見るだけで、最終的な振幅の感覚を得たいと考えています。
「この手順は非常に複雑で、積分は非常に難しいので、私たちがやりたいのは、グラフを見つめるだけで、最終的な答え、最終的な積分または周期についての洞察を得ることです」と Brown 氏は言いました.
保存
保存
驚きのつながり
周期と振幅は、1994 年にイギリスのオープン大学の物理学者である Kreimer と David Broadhurst によって初めて一緒に提示され、その後 1995 年に論文が発表されました。この研究により、数学者はすべての振幅がテートの動機の混合された周期であると推測するようになりました —ハーバード大学の名誉教授であるジョン・テイトにちなんで名付けられた特別な種類の動機で、すべての周期は、数論で最も影響力のある構造の 1 つであるリーマンのゼータ関数の複数の値です。電子-陽電子対が入り、ミューオン-反ミューオン対が出てくる状況では、振幅の主要部分は、3 で評価されるリーマン ゼータ関数の 6 倍になります。
すべての振幅が複数のゼータ値である場合、物理学者は、作業する数値の明確に定義されたクラスを得ることができます。しかし、2012 年、ブラウンと彼の共同研究者であるオリバー シュネッツは、そうではないことを証明しました。今日、物理学者が遭遇するすべての振幅はテートの動機が混ざり合った期間である可能性がありますが、「作品にスパナを投げ込む怪物がそこに潜んでいます」とブラウンは言いました。これらの怪物は「確かに生理ですが、人々が望んでいた単純で素敵な生理ではありません。」
物理学者と数学者が知っていることは、ファインマン ダイアグラムのループの数と、「重み」と呼ばれる数学の概念との間に関係があるように見えるということです。重みは、積分される空間の次元に関連する数値です。1 次元空間の周期積分は、0、1、または 2 の重みを持つことができます。 2 次元空間上の周期積分は、4 までの重みを持つことができます。重みは、周期をさまざまなタイプに分類するためにも使用できます。重みが 0 のすべての周期は代数的数であると推測され、多項式方程式の解になる可能性があります (これは証明されていません)。振り子の周期の重みは常に 1 です。 pi は重み 2 の周期です。また、リーマン ゼータ関数の値の重みは常に入力の 2 倍です (したがって、3 で評価されたゼータ関数の重みは 6 です)。
この重みによる周期の分類は、ファインマン ダイアグラムに引き継がれます。ファインマン ダイアグラムでは、ダイアグラム内のループの数がその振幅の重みに何らかの形で関連しています。ループのないダイアグラムの振幅は重み 0 です。ループが 1 つある図の振幅はすべてテートの動機が混在した期間であり、重みは最大でも 4 です。ループが追加されたグラフの場合、数学者は、たとえそれがまだ見えなくても、関係が続いていると考えています。
「より高いループに行くと、より一般的なタイプの周期が見られます」と Kreimer 氏は言います。 「数学者はテートの動機が混在していない動機についてあまり理解していないため、非常に興味を持っています。」
数学者と物理学者は現在、問題の範囲を確立し、解決策を作成するために行ったり来たりしています。数学者は、ファインマン ダイアグラムを記述するために使用できる関数 (およびその積分) を物理学者に提案します。物理学者は、数学者が提供しなければならない機能を凌駕する粒子衝突の構成を作成します。 「非常に技術的な数学的アイデアをいかに早く吸収したかを見るのは非常に驚くべきことです」と Brown 氏は述べています。 「物理学者に提供する古典的な数と関数が不足しています。」
自然のグループ
17 世紀に微積分学が開発されて以来、物理世界で発生する数は数学の進歩に情報を提供してきました。今日もそうです。物理学に由来する周期が「どういうわけか神から与えられ、物理理論に由来するという事実は、それらが多くの構造を持っていることを意味し、それは数学者が必ずしも考えたり、発明しようとしたりするとは限らない構造です」とブラウンは言いました.
Kreimer は、「自然が望む期間は、数学が定義できる期間よりも小さいセットであるように思われますが、このサブセットが実際に何であるかを明確に定義することはできません。」
ブラウンは、ファインマン ダイアグラムに由来する一連の周期に作用する一種の数学的群 (ガロア群) があることを証明しようとしています。 「これまでに計算されたすべてのケースで答えはイエスのようです」と彼は言いましたが、関係が完全に成り立つという証拠はまだ遠いです「物理学から得られた数値に作用するグループがあったというのが本当なら、それは対称性の巨大なクラスを見つけたことを意味します」とブラウンは言いました。 「それが本当なら、次のステップは、なぜこの大きな対称群が存在するのか、そしてそれがどのような物理的意味を持つのかを尋ねることです.」
とりわけ、それは 2 つの非常に異なるコンテキストからの基本的な幾何学的構成の間のすでに挑発的な関係を深めるでしょう:モチーフ、多項式方程式の解を理解するために 50 年前に数学者が考案したオブジェクト、および粒子の衝突方法の概略図であるファインマン図遊ぶ。すべてのファインマン図には動機が付随していますが、関連する図の構造について動機の構造が正確に何を言っているのかは、誰にもわかりません.