インダクタンス L と抵抗 R が交流電源に直列に接続されている場合、その回路は LR 回路または LR フィルターと呼ばれます。直列に接続されているため、両方に同じ量の電流が流れます。
LR 回路の個々の要素
組み合わせ回路に入る前に、個々の要素を簡単に見てみましょう。
抵抗のみが AC 電源に接続されている場合、式 I =Iosinwt で表される電位と同相の電流があり、電圧は V =Vosinwt です。 、したがって、電流の方程式は次のようになります。
I =Vo/R
インダクタのみが AC 電源に接続されている場合、電流は式 I =Iosin(wt- π/2) で表される電位より 900 遅れます。電圧は V =Vosin(wt) であるため、電流の式は I =V0/XL となります。ここで、XL は次の式で計算される誘導性リアクタンスです。
XL =2πfL で、単位はオーム (Ω) です
コンデンサのみが AC 電源に接続されている場合、電流は式 I =Iosin(wt+ π/2) で表される電位よりも 900 進んでおり、電圧は V =Vosin(wt) であるため、電流の式は I =V0/XC となります。ここで、XC は次の式で計算される容量性リアクタンスです。
XC =1/ 2πfC で単位はオーム (Ω)
LR回路
直列 LR 回路では、抵抗とインダクタンスが AC 電源に直列に接続されます。
ここで、抵抗に入る前に回路を流れる電流は i=i0sinwt です。
電流が抵抗に入ると、抵抗 VR の両端の電位差とインダクタ VL の両端の電位差は、時間とともに次のように表されます。
VR (t) =(V0)R sinwt (電流は抵抗の電位と同相であるため)
そして
VL(t) =(V0)L sin(wt+π/2) インダクタの場合、電流は電位より 900 遅れます
ここで、(V0)L はインダクタンスのポテンシャルのピーク値、(V0)R は抵抗のポテンシャルのピーク値です。
ここで、V0 は次のように計算できます:
(V0)2 =(V0)R2 + (V0)L2
(V0) =√( (V0)R2 + (V0)L2)
これは直列回路であるため、抵抗とインダクタンスを流れる電流は同じです。したがって
i0 =iL =iR
(V0) =√(i02R2 + i02XL2)
(V0) =√(i02 (R2 + XL2))
(V0) =i0 √ (R2 + XL2)
ここで √ (R2 + XL2) は一種の抵抗なので
(V0) =i0Z
ここで、Z は回路のインピーダンスとして知られています。
したがって、インピーダンスは、直列 RL 回路の電流の流れに対抗する抵抗 R とインダクタンス L の集合抵抗です。
フェーザ図によると、電流は RL 回路の電位より遅れていますが、純粋なインダクタ回路の場合ほど 90° 遅れていません。それは 0 から 90° の間のどこかです。この角度は Φ として知られています。
Φ の値は、フェーザー図で簡単に見つけることができます:
tanΦ =XL / R
ACの力率
通常、電力 P は次のように計算されます。
P =VI
しかし、AC 回路では、電圧 V と電流 I の両方が時間とともに変化します。したがって、瞬時電力 P(t) は次のように計算されます。
P(t) =V(t)I(t)
または
P(t) =V0sinwt I0(sinwt + Ф)
RL 回路は常に電流が電位よりも遅れている回路であり、力率は次の簡単な式を使用して計算されます
cosФ =R/Z
LR回路例
例 1:
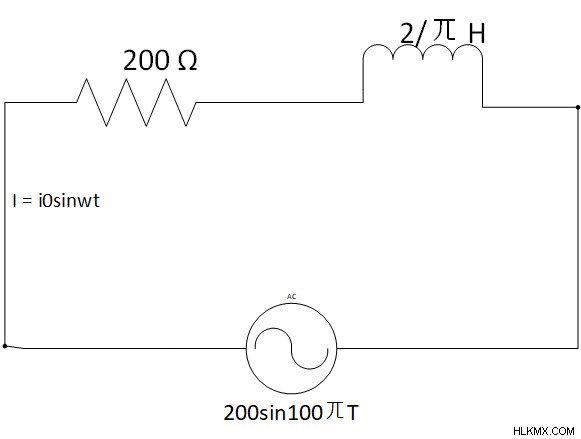この回路について、以下を見つけてみましょう:
誘導リアクタンス XL
インピーダンス Z
ピーク電流 i0
i(t)
解決策:
誘導リアクタンス XL
XL =wL =100ㄫ x 2/ㄫ =200 Ω
インピーダンス Z
Z =√ (R2 + XL2) =√((200)2 + (200)2 =200√2Ω
ピーク電流 i0
i0,=V0/Z =200/200√2 =1/√2 A
i(t) =i0sin(100ㄫt-Φ)
tanΦ =XL / R =200/200 =1
Φ =450
したがって、
i(t) =1/√2 sin(100ㄫt-ㄫ/4)
例 2:
次の回路を考えてみましょう:
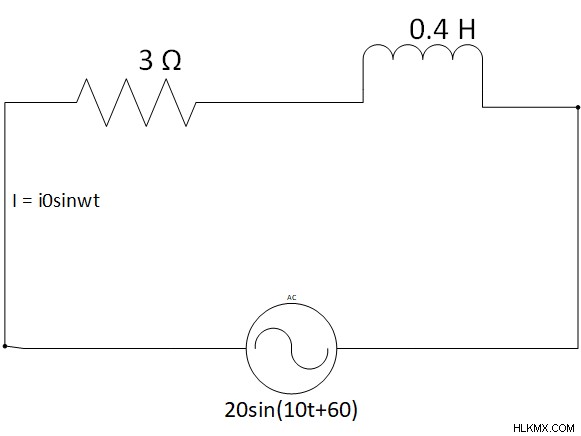
検索
XL
Z
I0
i(t)
VR(t)
VL(t)
解決策:
XL =wL =10 * 0.4 =4Ω
Z =√ (R2 + XL2) =√ (42+32) =5Ω
I0 =V0/Z =20/5 =4A
まず、これの Φ の値を計算しましょう
tanΦ =XL / R =4/3
Φ =530
i(t) =i0sin(10t + 600 – Φ)
i(t) =4sin(10t +600 – 530)
i(t) =4sin(10t + 70)
VR(t) =(V0)R sin(10t + 70)
(V0)R =i0R
=4 x 3
=12
VR(t) =12 sin(10t + 70)
VL(t) =(V0)L sin(10t + 70 + 900)
(V0)L =i0XL
=4 x 4
=16
VL(t) =16 sin(10t + 970)
結論
簡単な式と定義の助けを借りて、LR 回路を簡単に解くことができます。 LR 回路のインピーダンスは、電位からの電流の総遅延を決定する上で重要な役割を果たします。力率、Ф、w などのさまざまな側面が連携して、LR フィルターが効率的に機能します。
