逆微分または統合は、統合プロセスによってまとめられた一見無限に小さなデータの追加です。ギリシャ語の統合までさかのぼることは、ずっと前から数学のカリキュラムの一部でした。しかし、積分と微分の両方が逆演算であることが認識されたのは、ニュートンの時代でした。したがって、明確な形式のない複雑な形状は、統合の形式を使用して計算されます。簡単な形状の場合、式は常に有効です。ただし、定義できない構造は、積分を使用して計算されます。
統合記号は「∫」で表されます。
グラフ下の面積の計算
グラフの逆導関数または積分は、定義できない形状または定義できない形状の面積を計算するのに役立ちます。特定のものに拘束されない。曲面が関係する場合、計算は確かに難しくなります。したがって、基本的に、以下に示す曲線の面積を計算する必要がある場合:-
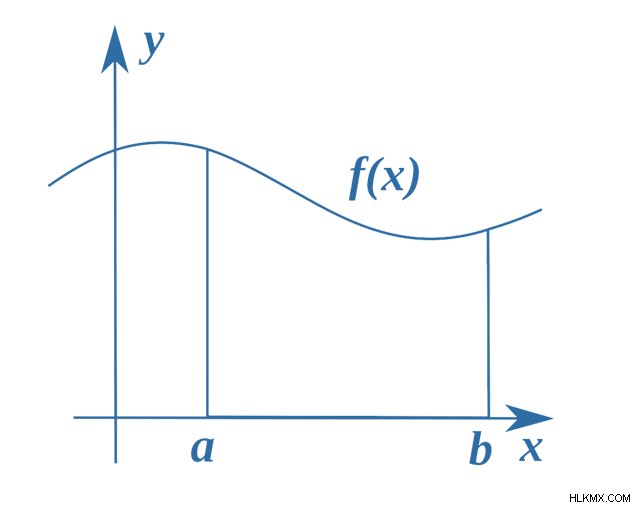
曲線の下の領域を見つける方法
曲線が x 軸に従って与えられている場合、次の方法でこれを解決する必要があります。 y=f(x) など。したがって、曲線 y の下の面積を求める公式は以下のとおりです。
abf(x)dx
面積の計算は次の手順で行われます:
A=baydx
A=baf(x)dx
A=[g(x)]ba
A=g(a)-g(b)
同様に、y 軸については逆です。ただし、関数は x=f(y):
A=baxdy
A=baf(y)dy
A=[g(y)]ba
A=g(a)-g(b)
ここで、g は方程式の積分関数を表します。ただし、これを計算するには、グラフ、方程式、および a や b などの値とともに、いくつかのデータまたは値が既に提供されている必要があります。
物理学への応用
誰もが知っているように、物理学は応用数学です。積分計算と面積計算の使用は、いくつかの物理値の値を計算するために非常に重要です。特に、ニュートンの法則や運動学や仕事などから派生した主題では重要です。どちらも曲線下面積の積分計算の驚くべき使用例です。
物理学の主なアプリケーションは
パスに沿って蓄積されたベクトルの量を調べる必要がある場合はいつでも、線積分が使用されます。古典的な例は、仕事が線積分 W=Fdx として表されることです
W=Fdx は、「パスに沿って作業を蓄積する」という考えを捉えていますですが、この概念は多くの場所に現れる可能性があります (矢印はベクトル係数と計算を決定し、スカラー積と混同しないように示されています)。
ガウスの法則は、線積分ではなく面積積分で表現されています。ここでのコンセプトは、「私はボールを持っており、ボールから出る電界の量を計算する必要がある」ということです。これは、ボールの各セクションから出るわずかな電場を計算し、それをすべて加算することによって行われます。これは当然、表面積分で行われます。
一般に、さまざまなベクトル量のグループがあり、単一の点よりも長い距離にわたって数値を計算する必要がある場合の場合、ある種のベクトル計算を行う可能性があります。物理学における面積積分の応用については、以下で詳しく説明します。
可変力によって行われる作業:-
W=Fx は、基本的な仕事関係の特定のケースであり、適用されるのは直線に沿った連続的な力。力 F が距離の関数としてプロットされる、表示される長方形の面積は、この接続によって決まります。距離とともに変化する力のより一般的な例では、仕事は曲線の下の面積として推定できます。たとえば、曲線の下の面積は、ばねを伸ばすために行われた作業の三角形の面積として簡単に計算できます。距離範囲全体の力の積分は力曲線の下の面積に等しいため、微積分も使用できます。
作業 =0xmF(x)dx =0xmkx dx =12kxm2>
ガウスの法則
ガウスの法則は電場に関するものではありませんが、電束;電界の式を決定するのに非常に役立ちます。電荷分布に特定の対称性 (球状、円筒状、または平面状) がある場合、電束の知識から電場を決定できます。電場が一定の振幅を持つこれらのシステムで、ガウス面 S、En=E を識別することができます。 En=-E は、E が表面のどこでも n に平行である場合にも当てはまります。 (表面的には、E と n がどこでも逆平行である場合、値は次のようになります。
=sE.ndA=EsdA =EA =qenc0
ここで文字は次を表します
E=電場,
n=コイルの巻き数
A=表面の面積、
q=同封の料金
0=真空の誘電率。
ベクトル計算
ベクトル計算では、スペースと3 次元空間での物体の必要な位置とその速度、および空間と次元に関連するその他のベクトル プログラムは、数学と物理学の両方のカリキュラムの計算の一部です。
結論
積分の適用は、この微積分が使用される分野によって決まります。曲線の下での積分では、一般に、振幅を持つ周期的な動きや、正弦関数または余弦関数の条件下で、適切に定義されていない形状の領域を見つけるために使用されます。このような関数は、積分の助けを借りずに計算することは難しいため、古い式や方法に依存するのではなく、積分を使用して計算する必要があります.