19 世紀の英国の数学者、オーガスタス・ド・モルガンによって与えられた 2 つの法則のセットは、ド・モルガンの定理と呼ばれます。 2 つの法則は、AND、NOT、および OR 関数の規則を使用します。これらの関数のプロパティを使用して、1 つのブール式をある形式から別の形式に変換できます。最初の定理は、積の反転は反転の和と同じであると述べています。 2 番目の定理は、和の逆数は逆数の積と同じであると述べています。ド・モルガンの定理は、変数が 2 つ以上ある場合にも成り立ちます。
最初の定理
De Morgan の最初の定理によると、2 つ以上の変数を AND してから補完すると、各変数の個別の補完の OR に等しくなります。ド・モルガンの第 1 の定理は、次のように記述できます。

真理値表を使用したド モルガンの第一定理の検証

最初の定理の実装
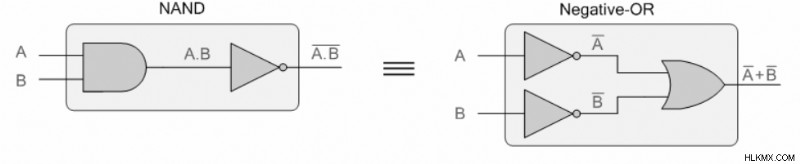
最初の定理の証明

 第二定理
第二定理
De Morgan の第 2 の定理によると、2 つ以上の変数を OR して補数をとると、各変数の個別の補数の AND に等しくなります。 2 番目のド モルガンの定理は、次のように記述できます。

真理値表を使用したド モルガンの第 1 の定理の検証

第二定理の実装
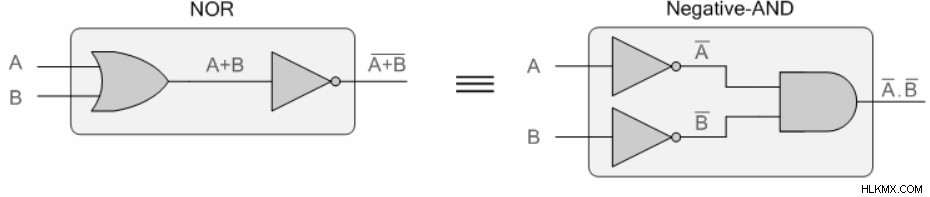
第二定理の証明


ド・モルガンの定理を使用した単純化
ド・モルガンの定理を使用して式を単純化するには、次の手順を使用します:
「OR」を「AND」に、「AND」を「OR」に置き換えます。つまり、式中の「+」を「・」に、「・」を「+」に置き換えます。
式の各用語を補完する
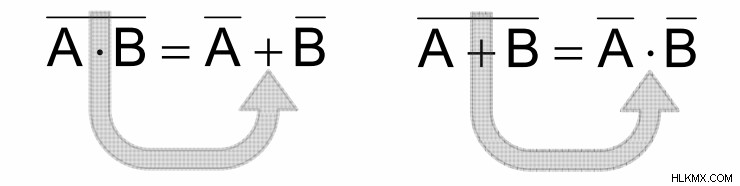
例 1

例 2
ド・モルガンの定理を使用した同等のゲート
ド・モルガンの定理を使用して同等のゲートを取得するには、AND ゲートを OR ゲートに置き換えます。逆もまた同様です。また、ゲートのすべての入力と出力を反転します。ド・モルガンの定理の例をいくつか見てみましょう。
例 1
基本的な AND ゲートを次のように考えてみましょう:
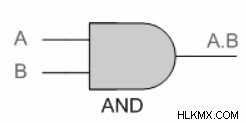
同等のゲートを見つけるには、次のように AND ゲートを OR ゲートに置き換え、NOT ゲートを使用して 2 つの入力と 1 つの出力を反転します。
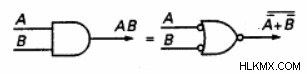
(入力と出力のバブルは反転を表します。)
次の真理値表を使用して、上記の式が等しいかどうかを確認してみましょう:
例 2
基本的な OR ゲートを次のように考えてみましょう:
同等のゲートを見つけるには、次のように OR ゲートを AND ゲートに置き換え、NOT ゲートを使用して 2 つの入力と 1 つの出力を反転します。
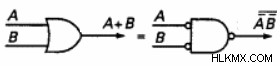
(入力と出力のバブルは反転を表します)
次の真理値表を使用して、上記の式が等しいかどうかを確認してみましょう: