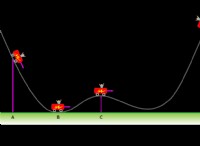
* 気分を無視する: 空気抵抗を無視しても、初期速度は打ち上げ角度に依存します。高速でまっすぐ上に打ち上げられたロケットは最終的に地球に戻り、初期速度が低いために浅い角度で打ち上げられたロケットは、水平方向にはるかに遠い距離を移動する可能性があります。
* 重力の影響: 重力は常にロケットを下に引っ張り、その軌跡に影響を与えます。ロケットが飛行中に長くなるほど、重大性の影響が大きくなります。
* その他の要因: 地球の回転、風の抵抗、およびロケット自身の推力プロファイルはすべて、軌道を決定する上で役割を果たします。
初期速度を計算するには、必要です:
1。起動角: ロケットが水平に比べて打ち上げられる角度。
2。ロケットのスラストプロファイル: ロケットのスラストが時間とともにどのように変化するか。
3。環境に関する情報: これには、空気密度、風の状態、地球の重力場などが含まれます。
単純化された計算(空気抵抗を無視):
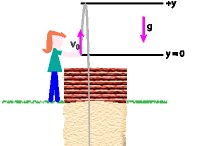
空気抵抗を無視し、一定の重力加速度(単純化)を想定すると、発射体運動方程式を使用できます。ただし、それでも、起動角度を知る必要があります。
例(単純化されたシナリオ付き):
仮定しましょう:
* 起動角: 45度(これにより、特定の初期速度の最大範囲が得られます)
* ターゲット距離: 1000 km
* 重力による加速: 9.8 m/s²
水平範囲に発射体運動式を使用してください:
`` `
範囲=(初期速度² * sin(2 *起動角) /重力による加速
`` `
これを再配置して、初期速度を解決できます。
`` `
初期速度=sqrt((範囲 *重力による加速) / sin(2 *起動角度))
`` `
値のプラグ:
`` `
初期速度=sqrt((1000000 m * 9.8 m /s²) / sin(90度))
`` `
`` `
初期速度≈3132m/s
`` `
覚えておいてください: これは非常に単純化された例です。現実世界のロケットの発売には、はるかに複雑な計算が必要であり、前述のすべての要因を考慮に入れています。