1。問題の設定
* 料金: 電荷-Eを備えた電子と電荷 +eのプロトンがあります。
* 力: それらの間の力は静電的であり、クーロンの法則によって与えられます:f =k *(e^2) / r^2、ここで
* kはクーロンの定数です(8.98755×10^9n⋅m^2/c^2)
* eは初等料金(1.602×10^-19 c)です
* rは、電子とプロトンの間の距離です。
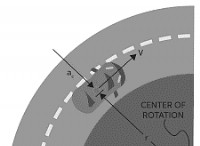
* 動き: 電子は輪になっています。つまり、それに作用する中心力がなければなりません。この力は、静電引力によって提供されます。
2。等しい力
静電力は、電子を円形軌道に維持する中心体の力です。
f_electrostatic =f_centripetal
* k *(e^2) / r^2 =m_e * v^2 / r
どこ:
* M_Eは電子の質量です(9.109×10^-31 kg)
* vは電子の速度です。
3。速度を解く
これで、電子の速度(V)を解くことができます。
* v^2 =k *(e^2) /(m_e * r)
* v =√(k *(e^2) /(m_e * r))
4。 BOHRモデルを使用して
最も単純なモデル(BOHRモデル)では、電子は量子化されたエネルギーレベルでプロトンを周回します。 最小の軌道(基底状態)の半径は以下によって与えられます。
* r =a_0 =5.29177×10^-11 m
ここで、a_0はbohr半径です。
計算
k、e、m_e、およびrの値を差し込む
V =√((8.98755×10^9n⋅m^2 / c^2) *(1.602×10^-19 c)^2 /(9.109×10^-31 kg * 5.29177×10^-11 m))
V≈2.19×10^6 m/s
重要な注意:
*上記の計算は、BOHRモデルに基づいて、水素原子の基底状態の電子の速度を与えます。このモデルは単純化であり、原子構造と量子力学の複雑さを完全に説明していません。
*実際には、電子の動きはより複雑であり、そのエネルギーレベルは完全に量子化されていません。 BOHRモデルは、原子構造の基本原理を理解するための有用な出発点を提供します。