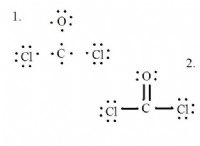$$ pv =nrt $$
どこ:
* Pは大気中の圧力(ATM)です
* vはリットルのボリューム(l)です
* nはガスのモル数です
* Rは理想的なガス定数(0.08206 L ATM / mol K)です
* tはケルビン(k)の温度です
まず、C2H2F4蒸気のモル数を計算する必要があります。
$$ n =\ frac {m} {m} $$
どこ:
* mはグラムのガスの質量(g)です
* mはモルあたりグラムのガスの臼歯質量(g/mol)
C2H2F4のモル質量は次のとおりです。
$$ m =2(12.01 \ g/mol) + 2(1.01 \ g/mol) + 4(19.00 \ g/mol)=64.06 \ g/mol $$
したがって、C2H2F4蒸気のモル数は次のとおりです。
$$ n =\ frac {0.100 \ g} {64.06 \ g/mol} =0.001561 \ mol $$
これで、P、N、R、Tの値を理想的なガス法則に置き換えて、ボリュームを計算できます。
$$ v =\ frac {nrt} {p} $$
$$ v =\ frac {(0.001561 \ mol)(0.08206 \ l atm / mol k)(295.45 \ k)} {0.0928 \ atm} $$
$$ v =0.404 \ l $$
したがって、0.0928 ATMおよび22.3°Cでの0.100 gのC2H2F4蒸気の体積は0.404 Lです。