1。位相変換:
* 固化: 微分方程式は、さまざまな相、微細構造、凝固速度の形成を含む、鋳造および溶接中の熱伝達と固化プロセスを説明しています。
* 降水硬化: 方程式は、合金における沈殿物の核生成と成長をモデル化し、その強度と硬さに影響します。
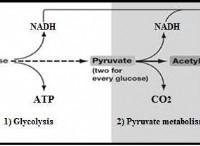
* 拡散: 微分方程式は、熱処理、合金化、および拡散制御反応を理解するために重要な金属内の原子の動きをモデル化します。
2。機械的挙動:
* クリープ: 方程式は、極端な条件で動作するコンポーネントを設計するために重要な高温での一定のストレス下での金属のゆっくりした変形を示しています。
* 疲労: 微分方程式は、金属の周期的な負荷と故障をモデル化し、疲労寿命を予測し、早期故障を防ぐのに役立ちます。
* プラスチック変形: 方程式は、降伏強度、ひずみ硬化、骨折など、ストレス下での金属の挙動を表しています。
3。処理:
* 熱処理: 微分方程式は、アニーリング、クエンチ、焼き戻しなどの熱処理プロセス中の熱伝達をモデル化するために使用され、微細構造と特性を最適化します。
* ローリングと押し出し: 方程式は、ローリングや押し出しなどの変形プロセス中の金属の流れを説明し、最終的な形状と特性を予測するのに役立ちます。
* パウダー冶金: 微分方程式は、粉末粒子を固体質量に統合することを含む焼結プロセスをモデル化します。
4。腐食:
* 電気化学腐食: 方程式は、腐食中に発生する電気化学反応を説明し、腐食速度の予測と保護コーティングの発生を可能にします。
* 応力腐食亀裂: 微分方程式は、ストレスと腐食性環境の相互作用をモデル化し、亀裂開始と伝播につながります。
5。微細構造の進化:
* 穀物の成長: 方程式は、多結晶材料の穀物の成長をモデル化し、機械的特性と性能に影響を与えます。
* 相変換: 微分方程式は、あるフェーズの別の相への変換を記述し、微細構造の進化と特性の変化を予測します。
冶金の微分方程式の例:
* 熱方程式: さまざまな冶金プロセスでの熱伝達をモデル化するために使用されます。
* 拡散方程式: 金属内の原子の動きをモデル化し、相変換、熱処理、合金を理解するために重要である。
* 応力 - ひずみ方程式: ストレス下の金属の機械的挙動を説明し、それらの変形と骨折の挙動に影響を与えます。
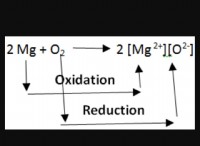
* 反応速度方程式: 酸化、還元、腐食を含む冶金反応の速度論をモデル化します。
結論:
微分方程式は、冶金学における広範囲の現象を理解し、予測する上で基本的な役割を果たします。これらの方程式を適用することにより、冶金学者は材料とプロセスを設計および最適化し、プロパティの改善、パフォーマンスの向上、および拡張コンポーネントの寿命につながることができます。