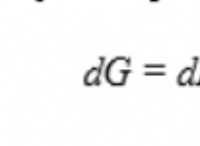1。同位体:
*要素には複数の同位体を持つことができます。複数の同位体は、同じ数のプロトン(要素を定義)であるが、異なる数の中性子を持つ原子です。中性子のこの違いは、各同位体の異なる原子質量につながります。
2。同位体の豊富さ:
*元素の各同位体は、特定の存在量(パーセンテージ)を持つ自然界に存在します。
3。計算:
*原子量は、元素のすべての同位体の質量の加重平均をとることによって計算されます。これはつまり:
* 各同位体の質量にその自然な存在量を掛けます(小数として)。
* すべての同位体の結果を合計します。
例:
塩素(CL)の例を見てみましょう。
* 同位体: 塩素には、塩素-35(35cl)と塩素-37(37cl)の2つの主要な同位体があります。
* 存在量: 35Clの豊富な75.77%、37clの豊富さは24.23%です。
* 質量: 35Clの質量は34.9689 AMU、37Clの質量は36.9659 AMUです。
計算:
*(34.9689 AMU * 0.7577) +(36.9659 AMU * 0.2423)= 35.453 AMU
したがって、塩素の原子量は35.453 AMUです。
キーポイント:
*原子量は、最も豊富な同位体の質量だけでなく、加重平均です。
*原子量は通常、周期表に表示されます。
*原子量は、平均化プロセスのために整数ではありません。
*原子量の単位は原子質量単位(AMU)です。
このプロセスにより、原子量は、異なる同位体とその相対存在量を考慮して、自然界に存在する要素の真の平均質量を反映することを保証します。