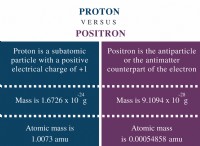
分子構造の考え方は、化学を理解するための基本です。おなじみの球と棒のモデルは、具体的であり、そのシンプルさが魅力的ですが、説明の価値という点では制限的であるか、誤解を招く可能性があります。 2 つの原子記号または物理的原子を接続する単純な線または棒としての化学結合の概念は、そのような誤解を招く結果の 1 つです。
特定の化合物の構造は、ほとんどの場合、X 線結晶構造解析によって決定されます。X 線結晶構造解析では、原子を取り囲む電子雲による光子の散乱が 回折パターン を作成します。 これにより、原子の位置が明らかになります。しかし、実験的な電子密度 (ρ ) は、分子の特定の形状を決定しない分子構造を生成します。つまり、電子の密度だけでは、原子を接続する特定の結合の存在を一意に説明することはできません。図 1 に示すような分子構造は、近接性と化学原子価の通常の規則に基づく原子間結合を反映しています。また、結合強度などの特性は推測できますが、軌道組成などのより基本的な特性にはアクセスできません。
波動関数 (ψ) は、量子力学 (QM) の基本的な概念であり、理論的には、特定の分子の完全な説明を表します。波動関数は確率振幅を表し、ψ は特定の位置にある粒子の確率密度を示します。特定の分子のシュレディンガー方程式を解くには、特定の核配置の電子波動関数を生成し (ボルン オッペンハイマー近似)、最適化された構造の電子 ψ を計算する前に核座標を個別に最適化する必要があります。特定の電子が 90% の確率で見つかる表面境界は軌道として定義され、局在する 2 中心結合または非局在化する多中心結合の組成を反映します。 QM 計算の品質は、通常は x 線または中性子回折によって決定される実験構造との比較によって評価できます。したがって、特定の結合の特性、つまりその軌道組成は、実験構造からではなく、理論から得られます。
最近の論文で、著者は ρ の間に実際に関係があることを実証することができました。 および ψ、つまり、以下の式 1 に示す等価性。
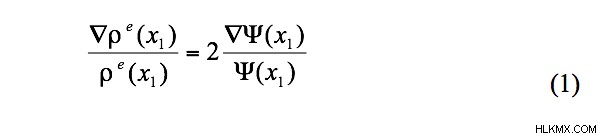波動関数 ψ(x 1 ) (1) は 1 電子波動関数と呼ばれ、シュレディンガー方程式のより厳密な全電子 ψ の近似値です。それにもかかわらず、(1) の関係の有用性は、実験的な電子密度 ρ を使用できることです。 、実験的なバージョンの ψ を視覚化します。具体的には、実験的に導出されたプロット
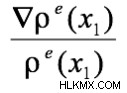
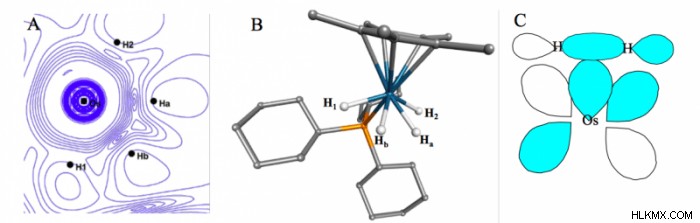
一電子波動関数 ψ(x のトポロジーまたは空間配置を表示します 1 ）。分子 [(C5 私5 )OsH4 (PCy3 )][BF4 ] 図 1 は、そのようなプロット、中性子回折によって決定された実験的構造、およびデュワー チャット ダンカンソン モデルとして知られるそのような相互作用の理論的説明を示しています。 「実験的」構造は、中央の金属原子と 4 つの水素すべての間のほぼ同等の結合を示しているという事実にもかかわらず、プロットされた実験バージョンの ψ(x 1 ）、またはρ (x 1 )、金属と Ha の間の異なる結合相互作用を示します と Hb , 金属と H1 の間で観測されたものより と H2 .従来の、より局所化された結合の図とは異なりますが、プロットは QM 理論によって予測されたモデルに著しく似ています。分子の場合 [FeH3 (PMe3 )4 ][BPh4 ] を図 2 に示します。
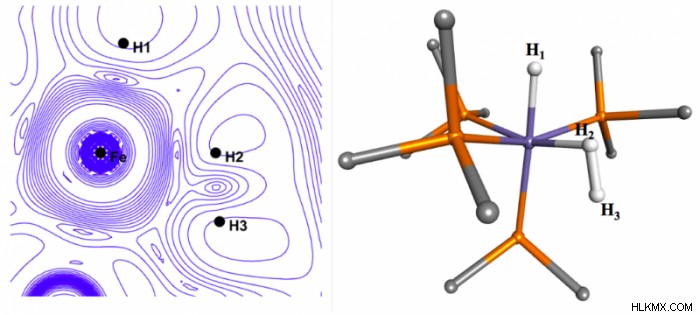ρのプロットに基づく解釈間の視点の違い (x 1 ) そして、単純に核間分離に基づくものはさらに顕著です。後者は H2 を示している可能性がありますが、 は金属中心と別の水素の両方に結合しています。ψ(x 1 )、または ρ (x 1 )、結合が図 1 とほぼ同じであることを示しており、ここでも QM 理論からの予測と一致しています。電子密度を使用して化学構造を解釈することは新しいことではありません。 分子中の原子の量子論 (QTAIM) として知られる形式主義は、分子の電子密度の分析を通じて局所化された化学結合のアイデアを取得することに基づいており、1998 年の化学ノーベル賞の一部は、密度汎関数の開発に対して授与されました。理論 (DFT)、ρ に基づくシュレディンガー方程式の解 基本変数としてのψではなく。でも。この作業は、実験的な ρ とリンクしています 視覚的で、広く適用可能で、うまくいけば有用な方法で、理論的な ψ を使用します。
これらの調査結果は、ジャーナル Computational and Theoretical Chemistry に最近掲載された「σ-配位複合体における分子波動関数の視覚化」というタイトルの記事で説明されています。 .この作業は、セント エドワーズ大学の Eamonn F. Healy によって実施されました。
参考文献:
<オール>
