数値計算は、科学の多くの分野で非常に重要であることが広く認識されています。非線形科学と複雑なシステムの多くの結論は、デジタル コンピューターでのシミュレーションで導き出されています。この重要性は広く認識されていますが、一般に、コンピュータの動作方法は詳細には知られていません.
次の例から議論を始めましょう。ロジスティック マップとして知られる次の式を考えてみましょう:
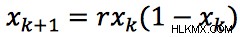
この方程式の背後にある考え方は非常に単純です。ステージ k =0 でシミュレーションを開始します。このステージでは、初期条件が設定されています。 r =4、および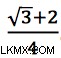 
次の段階で ¼ を計算するのは簡単です。 3回目の繰り返しの後、正解は行き詰まります— 固定 — ¾ の値で。
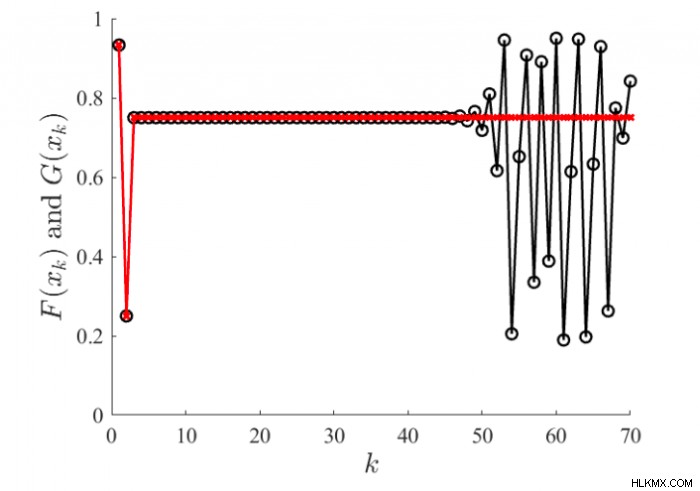
市販のソフトウェアを使用してこの計算を進め、図 1 の結果を得ることができます。赤い線と黒い線は、方程式 F によって生成されます。 (xk ) =4xk (1 – x k )、その間 G (xk ) =4xk – 4xk . 方程式は数学的に同等ですが、コンピューターは F に対して安定した固定された結果を生成し、G に対して無秩序な動作を生成します。非線形動的理論と、微積分と微分方程式のみに基づく数学の分野では、これを適切に説明できません。
「区分的アプローチを使用したマップの周期的軌道の間隔計算」というタイトルの最近の研究では、この状況を認識し、少なくともこの状況を減らすためのアプローチを開発しました。基本的な考え方は、浮動小数点に基づく数値計算の大部分が、基本的な算術演算に対してのみ、使用されるビット数に応じた精度内の結果、または技術用語で言えば、良好な結果を保証するように構築されているという事実に依存しています。 .
図 1 の例は、この例を非常に難しいものにする 2 つの機能を示しています。まず、計算は一連の基本的な算術演算です。第二に、そして最も重要なことは、最初の非常に小さなエラーが指数関数的に大きくなるという再発があります.私たちの論文では、関数のいくつかの機能を調べます。これにより、他のアプローチよりも一貫して結果の範囲を設定できます。この関数は区分関数と見なされます。一般に、提案された方法は、Intlab (Matlab ツールボックス) アプローチによって得られたものよりも大幅に狭い間隔を生成しました。ただし、私たちの方法ではかなり多くの反復が必要であることも明らかです。
関連研究
同じジャーナル「Detecting unreliable computer Simulations of recursive functions with interval extensions」に掲載された付随記事 https://doi.org/10.1016/j.amc.2018.02.020 では、このようなアイデアを使用して以前の結果のいくつかを示しました。コンピューターでの長時間のシミュレーションを保証するものは、現在のソフトウェアとハードウェアでは有効ではありません。また、記事「丸めモードと再帰的最小二乗アルゴリズムを使用した最大の正のリアプノフ指数の計算」、https://doi.org/10.1016 で、カオス システムを識別するための通常の機能であるリアプノフ指数を計算するために誤差伝播を利用します。 /j.chaos.2018.04.032.
今後の方向性
私たちは、コンピューターが科学と技術を発展させる素晴らしいツールであると確信しています。しかし、落とし穴を分析して回避できるようにするには、それらがどのように機能するかを理解する必要があることも確信しています.
これらの調査結果は、Applied Mathematics and Computation Applied Mathematics and Computation 誌に最近掲載された、区分的アプローチを使用したマップの間隔計算周期軌道というタイトルの記事で説明されています。 この作業は Erivelton G. Nepomuceno、 Heitor M. Rodrigues Junior、および Samir A.M.サン ジョアン デル レイ連邦大学の Martins 氏、マリボル大学と北京航空大学の Matjaž Perc 氏、マリボル大学の Mitja Slavinec 氏。
