複雑なシステムは、学生に困難をもたらす可能性があります。 2 つの異なるシステムが接続されている場合、いくつかの共通点があります。これらの接続を特定すると、問題の解決が容易になります。この問題例には、質量のない紐で接続された 2 つのブロックの複雑なシステムがあります。
問題例:
2 つのブロックは、摩擦のない滑車の周りにある質量のない糸でつながれています。ブロック A は摩擦のない表面を滑っていて、ブロック B が落ちるときに 2 番目のブロックに引っ張られます。
a) システムの加速度は?
b) 弦の張力は?
解決策:
この図は、ブロックの配置を示しています。
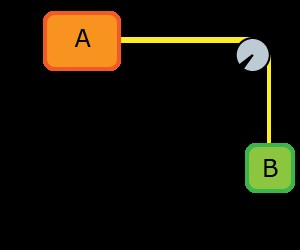
このシステムは、質量のないストリングによって結合されています。ブロック A が時間 t で距離 Δd だけ右に移動すると、ブロック B は下に Δd 移動します。つまり、ブロックの速度は同じです。
vA =⁄t =vB
速度方向は、各システムに選択された座標系によって調整できます。速度は常に同じなので、加速度も同じです。
a =aA =aB
弦は無質量なので、張力はシステム全体で均一です。ブロック A を横に引っ張る張力は、ブロック B を上に引っ張る張力と同じです。
両方のシステムの力を見つけてみましょう。
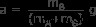
ブロック A から始めます。ブロック A は正の x 方向に加速されています。
ΣFx =T =mA a
ΣFy =N – mA g
ブロック A は垂直方向に動いていないので、その方向の力の合計は 0 に等しくなります。
ΣFy =N – mA g =0
N =mA g
次に、ブロック B にかかる力を見つけます。ブロック B は正の y' 方向に加速されており、x' 方向には力が作用していません。
ΣFy' =mB a
ΣFy' =mB g-T
これら 2 つの方程式を互いに等しく設定してください
mB a =MB g-T
これで、2 つの未知の変数を持つ 2 つの方程式ができました。これを解決する最も簡単な方法は、変数の 1 つについて 1 つの方程式を解き、その結果を 2 番目の方程式に代入して、他の変数について解くことです。 T の最後の方程式を解きましょう。
mB a =MB g – T
mB a – mB g =-T
T =mB g – mB
ブロック A の弦の張力を含む力の式にこの式を代入し、加速度を解きます。
T =mA a
mB g – mB a =mA
mB を追加 両側にa
mB g =mA a + mB
加速度を因数分解
mB g =(mA + mB )a
両辺を (mA + MB )
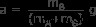
これで、質問のパート a に対する回答が得られました。これを使用して張力を見つけることができます。張力を含む方程式の 1 つに解を代入します。簡単なものを使ってみましょう:
T =mA a
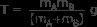
加速度が常に g 未満になることに注意してください。また、張力は常にブロック B の重量よりも小さいことに注意してください (mB g)。このタイプの問題でよくある間違いの 1 つは、弦の張力がブロック B の重量と等しいと仮定することです。これは、ブロック B が平衡状態にある場合にのみ当てはまります。ブロックが加速しているため、平衡状態にありません。