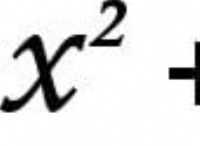ラテン語 (またはギリシャ語) の「centrum」と「gravitation」は、「centrum」と「gravitation」という言葉の語源です。重力は、天体を動かす宇宙の粒子間の重量または引力であり、中心 (重心) は天体の対角線の中央にある質量の中心です。
重心
重心 (「重い」を意味するギリシャ語の barrio に由来) としても知られる重心は、アイテムのポイント、またはオブジェクトのポイント (R、R、R1、または R2 で) のシステムです。全体の質量が集中しています。この考えにより、物体全体を、物体の総質量に等しい質量を持つ単一の物質点として見ることができます。力が作用しているかどうかに関係なく、任意の質点系には重心があります。重力が体に作用する場所は質量中心と呼ばれます。
方程式

w- オブジェクトの総重量。
d-重みの増分。
(粒子が固定された座標系を、x (または y) 軸を中心に 90 度回転させたものとして想像することで、z を取得できます)。
w=mg を知って、すべての粒子の重力による加速度 (g) が一定であると仮定すると (g は相殺されます)
質量の中心は、形状によっては、ボディの質量境界の外側にある場合もあります。三角形の重心は角二等分線の断面にありますが、立方体の重心は対角線の断面にあります。不規則な幾何学的物体の重心は、重力線の交点にあります。これは、総外力がパーティクル システムまたはボディに作用するポイントであり、システムのすべてのパーティクルまたは個々のボディ パーティクルから平均距離にあります。パーティクルまたはボディ システムが外力の影響下で移動する場合、重心があるポイントは、システムまたはボディのすべての質量が含まれているかのように移動します。物体の密度が均一でない場合、質量の中心 (重心) が物体の幾何学的中心にある必要はありません。

セントロイド
幾何学的中心は重心として知られています。簡単に言えば、体が均質な場合、重心は(密度が一定の場合)重心に対応します。同じアイテムのすべての質点の重力加速度のベクトルのコレクションの焦点は、物理学の物体の重心として定義されます。この点は、物体が均質である場合、重力線の接合点にあり、正しい幾何学的物体で幾何学的に定義されます。アルキメデスは、オブジェクトの重心を決定する方法を最初に説明しました。彼は、段ボールをオブジェクトの形に切り取り、それに複数の穴をあけることを提案しました。次に、壁の穴の 1 つに釘付けして、自由に吊るします。同じ釘で、垂れ下がる。鉛筆を使用して、鉛直の端の方向によって提供される方向を描きます。これは、オブジェクトの重心が置かれる場所です。他の穴で本体を交換し、手順を繰り返します。
重心と重心の違い
1.重力と重心の定義
重心は物体の幾何学的な中心であり、重心は体の総重量が作用する点です。重心とも呼ばれる重心は、体の全質量が集中する場所です。体のどの向きでも、ここに体の重力 (重量) が作用します。密度が均一なオブジェクトの場合、重心は重心です。
2.重力と重心の計算
質量 (および重量) がアイテム全体に均等に分布していない可能性があるため、重心の計算は簡単な作業ではありません。重心は、式 cg × W=S × dw を使用して計算できます。ここで、x は基準線からの距離、dw は重量増分、W はオブジェクトの総重量です。上で概説した鉛直線法などの方法を使用して、重心を見つけることができます。
覚えておくべきこと
重心は、重心とも呼ばれ、体全体の質量が集中する場所です。
式 W=s × dw を使用して重心を計算できます。
- W – 物体の総重量
- X- 基準線からの距離
- 重量の dw 増分。
重心は、密度が体全体に均等に分布しているオブジェクトの幾何学的中心の場所です。
重心は、鉛直線法または中央値の平均のいずれかを使用して計算されます。
これらの語句はどちらも、物体の重量、密度、およびバランスを定義するために使用されています。
結論
体の重心に向けられた、体の重量に等しい強さの合力の操作は、体の基本部分の重力を置き換えることができます.
重心は重力線の交点にあり、正しい幾何学的体で幾何学的に定義されます。物質の密度が体全体で同じであれば、これは正しいです。そのシナリオでは、体の重心は重心と同じです。
オブジェクトの重心は、そのすべてのポイントの平均位置です。切り取ったフォームが狂う可能性があるポイントです