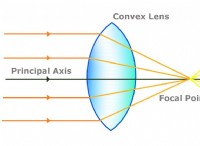
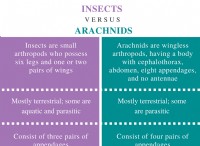
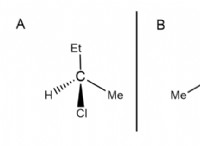
$$ s =ut+\ frac {1} {2} at^2 $$
どこ、
sは距離が落ちる(メートル)
Uは初期速度です(1秒あたりメートル)
Aは、重力による加速です(1秒あたりのメートルで四角)
tは(数秒で)時間です
この場合、オブジェクトは安静から落とされるため、初期速度は0 m/sです。重力による加速度は9.8 m/s^2です。そして、オブジェクトが128 mに落ちるまでの時間は、式を使用して見つけることができます。
$$ s =ut+\ frac {1} {2} at^2 $$
$$ 128 =0+\ frac {1} {2}(9.8)t^2 $$
$$ t^2 =\ frac {128} {4.9} $$
$$ t^2 =26 $$
$$ t =\ sqrt {26} =5.1 \ s $$
これで、最後の秒で距離が落ちる距離は、t =5 sとt =4 sを運動方程式に置き換えることで見つけることができます。
$$ s =ut+\ frac {1} {2} at^2 $$
$$ s =0(5)+\ frac {1} {2}(9.8)(5^2)$$
$$ s =\ frac {1} {2}(9.8)(25)=122.5 \ m $$
したがって、空気中の最後の秒の間に距離が落ちる距離は122.5 mです。