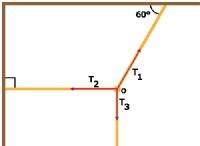
$$ a_c =\ frac {v^2} {r} $$
どこ:
- \(a_c \)は、1秒あたりのメートルでの中心細胞加速度\(m/s^2 \)です。
- \(v \)は、粒子の速度が1秒あたりのメートルで\(m/s \)です。
- \(r \)は、メートルの円形経路の半径\(m \)です。
中心性加速は、粒子が円形の経路で移動する原因です。求心性加速がなければ、粒子は直線的に移動します。
粒子の速度は一定ですが、その速度は、その速度の方向が常に変化しているためではありません。そして、それが中心の加速を引き起こすものです。