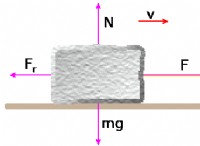
1。復元力:
*オブジェクトに作用する力は、平衡位置からの変位に直接比例する必要があります。
*力は常に平衡位置に向かって作用する必要があります。つまり、復元力です。
*数学的には、これは次のように表されます:f =-kx、ここでfは力、kはスプリング定数、xは変位です。
2。エネルギー損失なし:
*理想的には、摩擦、空気抵抗、またはその他の散逸力のためにエネルギー損失はないはずです。これにより、振動が無期限に続くことが保証されます。
3。線形回復力:
*復元力は線形でなければなりません。つまり、四角やその他の変位の力に依存しないことを意味します。これにより、振動が正弦波になることが保証されます。
4。単一平衡位置:
*システムには、単一の安定した平衡位置が必要です。これは、オブジェクトがこの位置から置換されると、それが平衡に向かって押し戻す力を経験することを意味します。
これらの条件の結果:
* 正弦波運動: SHMを受けるオブジェクトの変位、速度、および加速は、時間とともに正弦波によって異なります。
* 一定期間: 1つの完全な振動(期間)にかかる時間は、動きの振幅とは無関係に一定です。
* エネルギーの保存: システムの総機械エネルギー(ポテンシャルエネルギー +運動エネルギー)は一定のままです。
shmの例:
* 質量吸引システム: フックの法則に従う春に付随する塊。
* 単純な振り子: 小さなボブが、振動の小さな角度を想定して、明るい、柔軟性のないひもで固定点から吊り下げられました。
* LC回路: インダクタとコンデンサが直列に接続されており、コンデンサの電荷は正弦波を振動させます。
重要な注意:
理想的なSHMの条件が現実世界の状況で完全に満たされることはめったにありませんが、多くのシステムはほぼ単純な高調波運動を示し、物理学とエンジニアリングで非常に有用なモデルとなっています。