Centripetal Force:輪になって物事を動かし続ける力
ひもに結び付けられたボールが輪になって揺れていると想像してください。何かが円の中心に向かって引っ張っているので、ボールは直線で飛び立ちません。その「何か」は中心部の力です。
関係
中心力の方程式は次のとおりです。
f =(m * v^2) / r
どこ:
* f 中心部の力です(ニュートンで測定)
* m オブジェクトの質量です(キログラムで測定)
* v オブジェクトの速度です(1秒あたりのメートルで測定)
* r 円形経路の半径(メートルで測定)です
効果を分析しましょう
* 質量(m): より重いオブジェクト(より大きな質量)は、同じ速度で同じ円形経路で動き続けるために、より大きな中心力を必要とします。ひもに重いボールを考えてみてください。輪になって揺れ続けるには、より強く引っ張る必要があります。
* 速度(v): オブジェクトの速度が増加すると、必要な中心力も増加します。 これは、オブジェクトが方向をより迅速に変化させているため、円形の経路を維持するために強力な力が必要であるためです。ボールをより速く振るのを想像してみてください。弦の緊張が高まると感じるでしょう。
* radius(r): 円の半径が減少すると(オブジェクトがよりタイトな円で動いていることを意味します)、求心力が必要となります。ボールを手に近づけることを考えてみてください - あなたはそれを輪にするためにさらに強く引っ張る必要があります。
例:
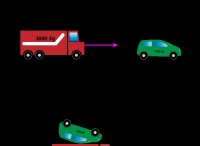
車が曲線を回ることを想像してみてください。
* より高い質量: より重いトラックでは、軽い車と同じ速度で曲線をナビゲートするためにより多くの中心力が必要です。
* 高速: 車が曲線の周りでスピードアップする場合、それを道路に保つために、より多くの求心力が必要です。
* 半径が小さい: より緊密な曲線(半径が小さい)には、より広い曲線よりも多くの中心的な力が交渉する必要があります。
キーテイクアウト:
中心力は、オブジェクトの速度の質量と正方形に直接比例し、円形経路の半径に反比例します。 オブジェクトが大きいほど、動きが速い、または曲線がより速くなるほど、より多くの中心力が必要になります。