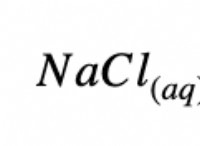
理想ガス 非理想的または実在気体 理想気体の法則から外れた気体です。別の見方をすると、理想気体は理論気体であり、実在気体は実際の気体です。ここでは、理想気体と実在気体の性質、理想気体の法則を適用するのが適切な場合、実在気体を扱うときに何をすべきかを見ていきます。
理想気体の法則
理想気体の法則は理想気体の法則に従います:
PV =nRT
P は圧力、V は体積、n は気体のモル数、R は気体定数、T は絶対温度です。
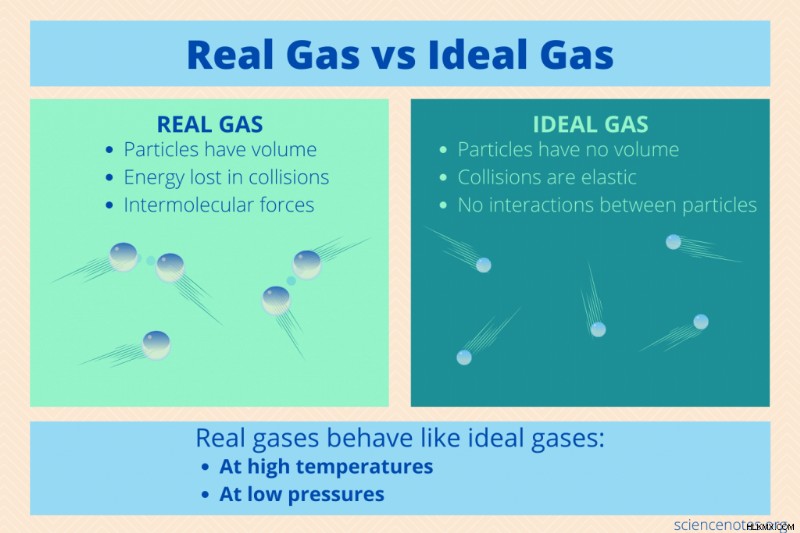
理想気体の法則は、化学的性質に関係なく、すべての理想気体に適用されます。ただし、これは特定の条件下でのみ適用される状態方程式です。これは、粒子が完全に弾性的な衝突に参加し、ボリュームがなく、衝突する以外に相互に作用しないことを前提としています。言い換えれば、気体は気体の運動分子理論に従って振る舞います。
実在気体と理想気体の類似性
実在気体と理想気体は、気体の特定の特性を共有しています:
- ミサ :実在気体粒子と理想気体粒子の両方に質量があります。
- 低密度 :気体は、液体や固体よりもはるかに密度が低くなります。ほとんどの場合、気体粒子は、理想気体と実在気体の両方で互いに遠く離れています。
- 低粒子量 :ガスは密度が高くないため、ガス粒子のサイズまたは体積は、粒子間の距離に比べて非常に小さいです。
- モーション :理想気体粒子と実在気体粒子の両方に運動エネルギーがあります。ガス粒子はランダムに移動し、衝突間はほぼ直線で移動します。
多くの実在気体は 2 つの条件下で理想気体のように振る舞うため、理想気体の法則は非常に便利です:
- 低気圧 :私たちが日常生活で遭遇する多くのガスは、比較的低圧です。粒子を近づけるのに十分なほど圧力が高い場合、圧力が要因になります。
- 高温 :ガスの場合、高温とは気化温度よりも十分に高い温度です。そのため、室温でさえも、実際の気体粒子に理想気体のように振る舞うのに十分な運動エネルギーを与えるのに十分なほど熱くなっています。
実在気体と理想気体
通常の条件下では、多くの実在気体は理想気体のように振る舞います。たとえば、空気、窒素、酸素、二酸化炭素、および希ガスは、室温および大気圧に近い理想気体の法則にほとんど従います。ただし、実際のガスが理想的なガスの挙動から逸脱する条件がいくつかあります:
- 高圧 :高圧により、ガス粒子が相互に作用するのに十分なほど接近します。また、分子間の距離が小さいため、粒子体積がより重要になります。
- 低温 :低温では、気体の原子や分子の運動エネルギーが小さくなります。それらは十分にゆっくりと移動するため、粒子間の相互作用と衝突中に失われるエネルギーが重要になります。理想気体は液体にも固体にも変化しませんが、実際の気体は変化します。
- 重ガス :密度の高い気体では、粒子同士が相互作用します。分子間力はより明白です。たとえば、多くの冷媒は理想気体のようには振る舞いません。
- 分子間力のあるガス :一部のガス中の粒子は、互いに容易に相互作用します。たとえば、水素結合は水蒸気中で発生します。
実際のガスは次の対象となります:
- ファンデルワールス軍
- 圧縮効果
- 可変比熱容量
- 変数構成
- 非平衡熱力学的効果
- 化学反応
実在気体と理想気体の違いのまとめ
| 違い | リアルガス | 理想ガス |
|---|---|---|
| パーティクル ボリューム | 一定量 | 量がない、またはごくわずか |
| 衝突 (コンテナとお互い) | 非伸縮性 | 弾性 |
| 分子間力 | はい | いいえ |
| 交流 | 粒子は相互作用し、反応する可能性があります | 衝突以外の相互作用なし |
| 相転移 | はい、相図によると | いいえ |
| ガス法 | ファンデルワールス方程式 | 理想気体の法則 |
| 現実世界に存在する | はい | いいえ |
理想気体の法則とファン デル ワールスの方程式
理想気体の法則が実在気体で機能しない場合、どのように計算を実行しますか? ファン デル ワールスの方程式を使用します .ファン デル ワールスの方程式は理想気体の法則に似ていますが、2 つの補正係数が含まれています。 1 つの係数が定数 (a ) 圧力値を修正して、ガス分子間の小さな引力を考慮します。もう 1 つの要因 (b ) は粒子体積の影響を考慮し、理想気体の法則の V を V – nb に変更します。 .
[P + a n/V](V – nb ) =nRT
a の値を知る必要があります そしてb ファン デル ワールスの式を使用します。これらの値は各ガスに固有です。理想気体に近い実在気体の場合、a そしてb はゼロに非常に近く、ファン デル ワールスの方程式を理想気体の法則に変えます。たとえば、ヘリウムの場合:a 0.03412 L-atm/mol と b 0.02370 L/mol です。対照的に、アンモニア (NH3 ):a は 4.170 L-atm/mol で、b は 0.03707 L/mol です。
a の値が大きいガス 沸点が高く、液化の値が低いものは絶対零度に近くなります。 b の値 はガス粒子の相対的なサイズを示すため、希ガス原子などの単原子ガスの半径を推定するのに役立ちます。
参考文献
- センゲル、ユヌス A.、マイケル A. ボールズ (2010)。 熱力学:工学的アプローチ (第 7 版)。マグロウヒル。 ISBN 007-352932-X.
- Tschoegl, N.W. (2000). 平衡および定常熱力学の基礎 .アムステルダム:エルゼビア。 ISBN 0-444-50426-5.
- タッカーマン、マーク E. (2010)。 統計力学:理論と分子シミュレーション (第 1 版)。 ISBN 978-0-19-852526-4.
- Xiang, H. W. (2005). 対応状態の原理とその実践:流体の熱力学、輸送、および表面特性 .エルゼビア。 ISBN 978-0-08-045904-2。