円錐振り子の理解
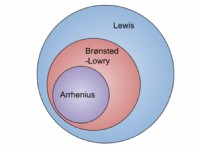
円錐振り子は、円錐形をたどる輪を丸くする単純な振り子です。主要なコンポーネントがどのように関連するかは次のとおりです。
* 角度(θ): 文字列と垂直の間の角度。
* 長さ(l): 文字列の長さ。
* radius(r): 円形経路の半径。
* 期間(t): 1つの完全な革命にかかる時間。
* 速度(v): 円形の経路に沿ったボブの一定速度。
θが90度に近づいているときの制限
角度θが90度に近づくと、次のことが発生します。
* 半径(r)が増加します: ボブはさらにスイングし、円形の経路の半径を大きくします。 `r =l * sin(θ)`、θが90度に近づくと、sin(θ)が1に近づき、rがLに近づくため。
* 期間(t)が無限に近づく: 円錐振り子の期間の式は次のとおりです。
`` `
t =2π√(l * cos(θ) / g)
`` `
ここで、「G」は重力による加速です。 θが90度に近づくと、cos(θ)が0に近づきます。これは、期間tが無限に大きくなることを意味します。本質的に、ボブは1つの革命を完了するのに無限に長い時間がかかるでしょう。
* 速度(v)がゼロ:に近づきます ボブの速度は次のように与えられます:
`` `
v =2πr / t
`` `
期間tが無限に近づくと、速度Vはゼロに近づきます。これは理にかなっています。なぜなら、ボブは、サークルを完成させるのに時間がかかり、時間がかかるため、本質的に遅くなって動いているからです。
実際的な意味
実際には、円錐振り子は本当にθ=90度に達することができません。
* 弦の張力: 弦の緊張は、90度でボブの重量をサポートするために無限に大きくなる必要があります。 本当の文字列は壊れます。
* 重力: ボブは最終的に重力のために倒れ、90度にとどまるのを防ぎました。
キーテイクアウト
角度θが円錐振り子で90度に近づくと、期間は無限に大きくなり、速度はゼロに近づきます。これは、物理的な制約のために実際には達成できない理論的な制限です。