移動ポイント料金のBiot-Savart Law
磁場 b 点で r 速度 v で移動する電荷 * q *のため によって与えられます:
`` `
b(r) =(μ₀ /4π) *(q * v × r̂ ) /r²
`` `
どこ:
* μ₀ 自由空間の透過性(約4πx10⁻⁷T⋅m/a)です
* r̂ 電荷の位置からポイント r を指すユニットベクトルです フィールドを計算している場合。
* r 電荷とポイントの間の距離 r 。
* × クロス製品を示します。
説明:
* 方向: 磁場 b 両方の速度ベクトル v に垂直です 充電から観測点を指すベクトル r 。これは、クロス製品の直接的な結果です。
* 大きさ: 磁場の強度は、電荷からの距離の平方に反比例します。
* 速度依存性: 磁場は、電荷の速度に直接比例します。固定電荷は磁場を生成しません。
重要な考慮事項:
*この式は、自由空間を移動する単一ポイント電荷に適用されます。
*複数の料金がある場合、または料金が複雑な方法で移動している場合は、Biot-Savartの法則を個々の料金に適用し、結果のフィールドを重ねて総磁場を見つける必要があります。
例:
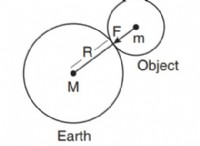
x軸に沿って速度 * v *で移動する電荷 * q *があるとしましょう。 y軸の電荷の真上の点で、電荷からの距離 * d *で磁場を見つけたいです。
1。 r: ベクトル r 充電から観測点までのポイント、 r =(0、d、0)。
2。 r̂: ユニットベクトル r̂ r です / | r |、(0、1、0)です。
3。 v: 速度ベクトルは v です =(v、0、0)。
4。 v×r̂: クロス製品は(0、0、v)です。
ここで、これらの値をBiot-Savart Lawに差し込みます。
b =(μ₀ /4π) *(q *(0、0、v) /d²)=(μ₀qv /4πd²) *(0、0、1)
磁場は、速度と位置ベクトルの両方に垂直な正のz方向を指します。