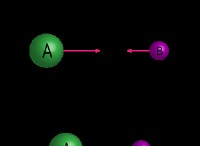
y(x、t)=sin(kx -ωt +φ)
どこ:
* y(x、t) 位置 *x *と時間 *t *での波の変位は
* a 波の振幅です(平衡からの最大変位)
* k 波数(2π/λ、ここでλは波長)です。
* ω 角周波数です(2πf、ここでfは周波数です)
* φ 位相定数です(t =0での波の初期位置を決定します)
用語の説明:
* 振幅(a): この値は、その平衡位置からの波の最大変位を決定します。
* 波数(k): これは、特定の距離(通常は2π)にどの波長が適合するかを説明します。式k =2π/λによる波長(λ)に関連しています。
* 角度周波数(ω): これは、波がどれだけ速く振動するかを表しています(1秒あたりのラジアンで)。式ω=2πfによる周波数(f)に関連しています。
* 位相定数(φ): これにより、波が水平にシフトし、時間t =0での初期位置が決まります。
なぜ正弦波関数が横波を表すのに適しているのか:
* 周期的な動作: 横波は周期的な動きを示し、正弦波関数は自然に周期的な挙動を表します。
* 単純な表現: 正弦波関数は、横波の本質的な特徴をキャプチャできる比較的単純な数学的式です。
* 柔軟性: パラメーターa、k、ω、およびφは、異なる振幅、波長、周波数、および位相を持つさまざまな横波をモデル化するように調整できます。
例:
0.1 mの振幅、0.5 mの波長、2 Hzの周波数、およびπ/4の初期相を持つストリングに沿って移動する横波を考えてみましょう。この波の方程式は次のとおりです。
y(x、t)=0.1 sin(4πx -4πt +π/4)
この方程式は、waveの振幅、波長、周波数、および初期位相をキャプチャして、任意の位置と時間での弦の変位を正確に表します。
注:
このモデルは、実際の横波の単純化された表現です。実際には、波はより複雑であり、正弦波パターンに完全に従うことはできません。ただし、このモデルは、横波の動作を理解し分析するための有用なフレームワークを提供します。