弾性衝突は、運動量と運動エネルギーの両方が保存されるオブジェクト間の衝突です。この弾性衝突の例の問題は、弾性衝突後の 2 つの物体の最終速度を見つける方法を示します。
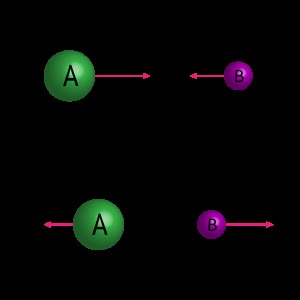
この図は、2 つの質量 A と B の間の一般的な弾性衝突を示しています。関連する変数は次のとおりです。
mA は物体 A の質量
Vあい は物体 A の初速度
VAf はオブジェクト A の最終速度です。
mB は物体 B の質量
VBi は物体 B の初速度、
VBf はオブジェクト B の最終速度です。
初期条件がわかっている場合、システムの総運動量は次のように表すことができます
衝突前の全運動量 =衝突後の全運動量
または
mA Vあい + mB VBi =mA VAf + mB VBf
システムの運動エネルギーは
衝突前の運動エネルギー =回収後の運動エネルギー
½mA Vあい + ½mB VBi =½mA VAf + ½mB VBf
これらの 2 つの方程式は、最終速度について次のように解くことができます。
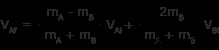
と
これらの方程式にたどり着く方法を確認したい場合は、2 つの質量の弾性衝突 – 演習で示すことができますを参照して、段階的な解決策を確認してください。
弾性衝突の例の問題
2 m/s で移動する 10 kg の質量が、反対方向に 4 m/s で移動する 2 kg の質量と弾性的に衝突します。両方のオブジェクトの最終速度を見つけてください。
解決策
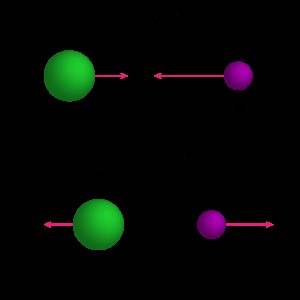
まず、問題を視覚化します。この図は、条件についてわかっていることを示しています。

2 番目のステップは、参照を設定することです。速度はベクトル量であり、速度ベクトルの方向を区別する必要があります。左から右を「正」の方向として選択します。右から左に移動する速度には、負の値が含まれます。
次に、既知の変数を識別します。私たちは次のことを知っています:
mA =10kg
Vあい 2メートル/秒
mB =2kg
VBi =-4 メートル/秒。負の符号は、速度が負の方向にあるためです。
次に、VAf を見つける必要があります と VBf .上記の方程式を使用します。 VAfから始めましょう .
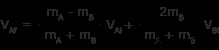
既知の値を組み込みます。
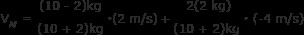
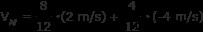

VAf =0 メートル/秒
より大きな質量の最終速度はゼロです。衝突により、この質量は完全に停止しました。
VBf

既知の値を組み込む



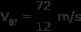
VBf =6 メートル/秒
答え
2 番目の小さい方の質量は 6 m/s で右 (答えの正符号) に飛び出し、最初の大きい方の質量は弾性衝突によって宇宙で完全に停止します。
注:2 番目のステップで基準フレームを反対方向に選択した場合、最終的な答えは VAf になります。 =0 m/s および VBf =-6 メートル/秒。衝突は変わらず、答えのサインだけが変わります。数式で使用する速度値が参照フレームと一致していることを確認してください。