概念とそのアプリケーションの内訳は次のとおりです。
1。微分とは?
* 無限変化: 微分は、変数のわずかに小さな変化を表します。多くの場合、xの小さな変化の「dx」のような変数が続く「d」で示されます。
* 変化率: 微分は、導関数の概念に密接に関連しています。関数の導関数は、入力変数に関してその関数の変化の瞬間的な速度を示します。
2。物理学の例:
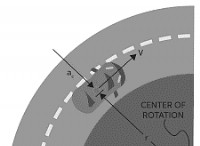
* 変位と速度: 移動オブジェクトがある場合、その位置(変位)は時間とともに変化します。変位の微分「DX」は、位置の小さな変化を表しています。この変化を時間の変化(dt)で除算すると、瞬時速度:dx/dt =vが取得されます。
* 力と加速: 速度の微分「DV」は、速度の小さな変化を表します。この変化を時間の変化(dt)で割ると、dv/dt =a。
* 作業とエネルギー: オブジェクトで行われた作業は、適用された力に移動距離を掛けた力に等しくなります。変位「dx」と力「f」に小さな変化がある場合、その小さな変位で行われた作業は「f * dx」です。
3。キーアプリケーション:
* 動きの理解: 微分は、動きを詳細に説明するために不可欠です。これは、速度と加速度が時間の経過とともにどのように変化するかを分析できるためです。
* フィールドの分析: 微分は、電界や磁場などのフィールドを理解するのに使用されます。
* 方程式の解決: ニュートンの第二法則(f =ma)のように、多くの物理方程式は微分を使用して表されます。これらの方程式を解くために、微分を含む計算手法を使用します。
要約:
微分は物理学の強力なツールであり、物理的な量と互いにどのように変化するかの複雑な関係を分析することができます。それらは、運動、力、フィールド、および物理的世界の他の多くの側面を理解するための基本です。