熱力学の初期段階では、研究者は熱と仕事の移動の研究に重点を置いていました。工学、大気科学、天体物理学などのさまざまな分野で考慮される熱放射は、熱理論の概念を使用して長い間扱われてきました。
ここ数十年で、科学者は、放射線貯留層が温度だけで特徴付けられるのではなく (熱貯留層のように)、化学ポテンシャルや形態係数などの他のパラメーターによっても特徴付けられることを徐々に理解するようになりました ([1A] を参照)。熱放射の最も成功したモデルは、Planck [2A] の精力的な研究に由来し、黒体放射 (BBR) の仮説に基づいています。
過去数十年間、多くの著者が熱放射エネルギーの仕事への変換を研究しましたが、これは主に太陽エネルギーの利用への影響によるものです。 BBR の特定のケースに対して最も重要な研究努力がなされ、顕著な結果が得られました。変換効率を最大にするための最初の選択肢は、カルノーの関係です [7B]:
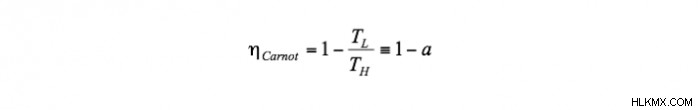
どこで TH そしてTL は、それぞれ放射線貯留層と環境の温度です。減少した環境温度 a の定義 (≡TL /TH ) は式で使用されています。 (1b)。もう 1 つの選択肢は、Petela [8B]、Landsberg [9B]、および Press [10B] によって個別に導出された次の関係です (PLP 効率):
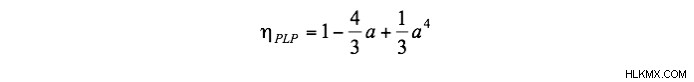
これらの効率の上限は、放射線貯留層と環境の温度のみの関数であり、一般的ではないことが最近証明されました。実際、放射貯留層は温度に加えて他のパラメーターによって特徴付けられ、これらのパラメーターの値の違いは、変換効率値の違いをもたらすと予想されます。たとえば、カルノーと PLP の効率は 半球 にのみ適しています。 BBRのリザーバー[11B、12B、18A]。 [11B、12B] では、任意のビュー ファクターの BBR 貯留層について、より一般的な上限効率式が導出されており、カルノーおよび PLP 効率は、まさに特殊なケースです [18A]。たとえば、BBR 貯留層が放射線エネルギー変換器から幾何学的 (ビュー) 係数 f で見える場合 H 、変換効率の上限は [11B,12B]:
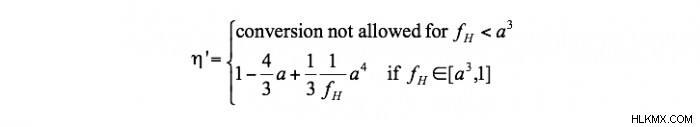
制約 fH > a エントロピー生成のない仮説的なエネルギー変換プロセスの仮定から来ています。特定のケースでは fH =a 、式。 (3) は、カルノー効率の式 (1) に還元されます。 (1a、b)。半球状の BBR リザーバーの場合 fH =1 および式(3) は、PLP 効率の式 (1) に還元されます。 (2)。上限 η' は、放射エネルギーをに変換するために機能します。 仕事 、熱を仕事に変換するときにカルノー効率が果たすのと同じ役割 考えられている。実際、カルノー効率は熱貯蔵庫と冷熱貯蔵庫の温度のみに依存するという事実にもかかわらず、任意の運転体制での実際の熱機関の効率よりも高くなります。
黒体放射は有用な理論ツールです。ただし、自然界では、光子エネルギー レベルあたりの平均占有数が黒体放射の占有数と正確に一致することはめったにありません。このような場合、熱放射は希釈としてより適切にモデル化されます BBR。希釈熱放射のよく知られた例は、拡散太陽放射と、灰色の太陽熱収集器から放出される放射です。希釈された BBR は、希釈係数 ε <1 によって特徴付けられます。地球大気の外側の太陽放射は、希釈されていない黒体放射 (ε =1) としてモデル化できます。地表での太陽放射は、直接放射 (太陽の方向から直接来る) または拡散放射 (いくつかの散乱の後、天蓋のさまざまな領域から受け取られる) のいずれかです。吸収のため、直達日射と拡散日射の両方が希釈 BBR としてモデル化される可能性があり、希釈係数は一般に互いに異なります。
希釈 BBR の熱力学は、Landsberg と Tonge による重要な論文で扱われています [14B、15B]。過去数十年間、何人かの著者が大気中の多重散乱太陽放射の物理 [16B]、伝導と放射によって伝達されるエントロピー フラックスの分析 [17B]、大気プロセス [18B,19B]、表面による熱放射 [20B]、地表面での太陽放射のエクセルギーの推定 [21B]。
ただし、希釈された BBR エネルギーの仕事への変換はほとんど考慮されていません。カルノー効率と PLP 効率は、放射線エネルギー変換器が 希薄 BBR エネルギーは仕事を生成できません。
最近の論文で、希釈 BBR の高温貯留層からの仕事抽出の単純なモデルを開発しました。シンクは熱貯留層です。最も関連性の高いプロセスがモデルに含まれており、これらのプロセスの不可逆性が考慮されています。効率の上限は、完全に可逆的なエネルギー変換の仮説の下で得られる可能性があります。
可逆性の仮定を緩和することにより、より正確な (つまり、より低い) 上限が得られます [21A]。これは、Gouy-Stodola の定理 [1A] の直接的な結果です。 灰色の特定のケース 人体への放射線が考慮されています。いくつかの詳細が続きます。吸収体は希釈係数 εH の希釈放射線を受け取ります 放射線貯蔵庫から。吸収体の吸収率は αa 吸収体は希釈係数 εa の希釈 BBR を放出します 幾何学的因子 fa の下で .重要なパラメータは、以下によって定義される相互作用係数 ι です。

重要な結果は、次の上限効率 η です:
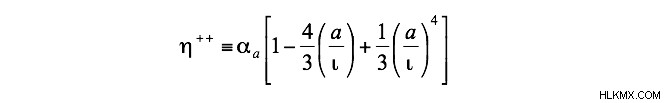
η は、希釈された放射の高温放射貯留層と低温熱貯留層の間で動作する放射エネルギー変換器の変換効率の解析的な上限効率を構成します。 η は α によって特徴付けられる大規模なクラスの状況に使用できます ≤ ι ≤ 1;このクラスには、PLP 効率が導き出された状況が含まれます (つまり、エネルギーが 希釈されていない そして完全に集中 BBRは黒体を使用して吸収されます 半球状に放射する吸収体 、 ι =1)。 η は、Carnot および PLP の効率よりも正確です。上限効率 η は、高温および低温の熱貯蔵庫の温度、ならびに放射貯蔵庫の希釈係数と幾何学的係数、および吸収体の性質(つまり、放出された放射の吸収率、放射率、幾何学的係数)に依存します。しかし、η は実際の放射線エネルギーを仕事に変換する効率よりも高くなっています。
これらの調査結果は、「希釈された太陽放射からどのくらいの仕事を抽出できるか?」というタイトルの記事で説明されています。最近、Solar Energy誌に掲載されました。 この作業は、ブカレスト工科大学とルーマニア アカデミーの Viorel Badescu によって行われました。
参考文献:
<オール>