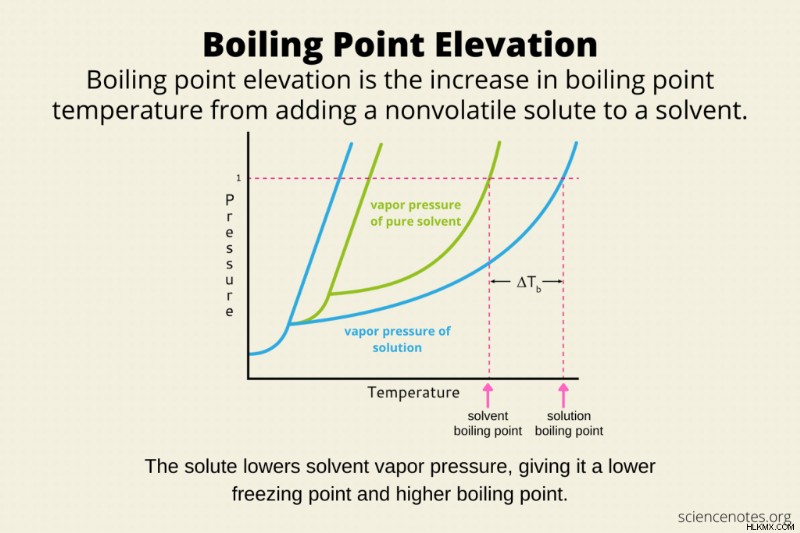
沸点上昇 不揮発性溶質を溶媒に溶解することによる溶媒の沸点の上昇です。例えば、塩を水に溶かすと水の沸点が上がり、100℃以上になります。凝固点降下や浸透圧と同様に、沸点上昇は物質の結合特性です。言い換えれば、効果は、溶質の性質ではなく、溶媒に溶解する溶質粒子の数に依存します。
沸点上昇の仕組み
溶質を溶媒に溶解すると、溶媒の上の蒸気圧が低下します。沸騰は、液体の蒸気圧がその上の空気の蒸気圧と等しくなったときに起こります。したがって、液体から気相に移行するのに十分なエネルギーを分子に与えるには、より多くの熱が必要です。つまり、沸騰はより高い温度で発生します。
理由 これが起こるのは、溶質粒子が揮発性ではないためです。そのため、いつでも、気相ではなく液相にある可能性が最も高くなります。溶質が溶媒を希釈することもあり、沸点上昇は揮発性溶媒でも発生します。余分な分子は、溶媒分子間の相互作用に影響します。
電解質は沸点上昇に最も大きな影響を与えますが、溶質の性質に関係なく発生します。塩、酸、塩基などの電解質は、溶液中でイオンに分解されます。溶媒に加える粒子が多いほど、沸点への影響が大きくなります。たとえば、砂糖は塩 (NaCl) よりも効果が低く、塩化カルシウム (CaCl2) よりも効果が低くなります。 )。砂糖は溶けますが、イオンには解離しません。塩は 2 つの粒子 (Na と Cl) に分解され、塩化カルシウムは 3 つの粒子 (1 つの Ca と 2 つの Cl) に分解されます。
同様に、濃度の高い溶液は、濃度の低い溶液よりも沸点が高くなります。たとえば、0.02 M NaCl 溶液は 0.01 M NaCl 溶液より沸点が高くなります。
沸点上昇式
沸点式は、溶媒の標準沸点と溶液の沸点の温度差を計算します。温度差は沸点上昇定数です (K
ΔT =K
沸点式の別の形式では、クラウジウス-クラペイロンの式とラウールの法則を使用します。
ΔTb =モル濃度 * K
ここで、i はファントホッフ因子です。ファントホッフ係数は、溶質 1 モルあたりの溶液中の粒子のモル数です。たとえば、砂糖は溶解しますが解離しないため、水中のスクロースのファントホッフ係数は 1 です。水中の塩と塩化カルシウムのファントホッフ係数は、それぞれ 2 と 3 です。
注:沸点上昇の式は、希薄溶液にのみ適用されます。集中ソリューションに使用できますが、おおよその答えしか得られません。
沸点上昇定数
沸点上昇定数は、1モル溶液の沸点の変化である比例係数です。 K
| 溶媒 | 標準沸点、C | K |
| 水 | 100.0 | 0.512 |
| ベンゼン | 80.1 | 2.53 |
| クロロホルム | 61.3 | 3.63 |
| 酢酸 | 118.1 | 3.07 |
| ニトロベンゼン | 210.9 | 5.24 |
沸点上昇問題 – 水への塩の溶解
たとえば、31.65 g の塩化ナトリウムを 220.0 mL の水に溶かした溶液の沸点を 34 °C で求めます。すべての塩が溶解すると仮定します。 35 °C での水の密度は 0.994 g/mL で、K
道徳の計算
最初のステップは、塩溶液のモル濃度を計算することです。周期表から、ナトリウム (Na) の原子量は 22.99、塩素の原子量は 35.45 です。塩の式は NaCl なので、その質量は 22.99 プラス 35.45 または 58.44 です。
次に、存在する NaCl のモル数を決定します。
NaCl のモル数 =31.65 g x 1 mol/(22.99 + 35.45)
NaCl のモル数 =31.65 g x 1 mol/58.44 g
NaCl のモル =0.542 mol
ほとんどの問題では、水の密度は基本的に 1 g/ml であると仮定します。次に、塩濃度はモル数を水のリットル数で割った値 (0.2200) です。しかし、この例では、水温が十分に高いため、密度が異なります。
kg 水 =密度 x 体積
kg 水 =0.994 g/mL x 220 mL x 1 kg/1000 g
kg 水 =0.219 kg
mNaCl =NaCl のモル数/kg 水
mNaCl =0.542mol/0.219kg
mNaCl =2.477 モル/kg
ファントホッフ係数を見つける
非電解質の場合、バント ホッフ係数は 1 です。電解質の場合、溶質が溶媒中で解離するときに形成される粒子の数です。塩は 2 つのイオン (Na と Cl) に解離するため、ファントホッフ係数は 2 です。
沸点上昇式を適用
沸点上昇式は、新しい沸点と元の沸点の温度差を示します。
ΔT =iK
ΔT =2 x 0.51 °C kg/mol x 2.477 mol/kg
ΔT =2.53 °C
新しい沸点を見つける
沸点上昇式から、新しい沸点は純粋な溶媒の沸点よりも 2.53 度高いことがわかります。水の沸点は 100 °C です。
溶液の沸点 =100 °C + 2.53 °C
溶液の沸点 =102.53 °C
水に塩を加えても、沸点は大きく変わらないことに注意してください。水の沸点を上げて料理を早く調理しようとすると、塩分が多すぎてレシピが食べられなくなります!
参考文献
- Atkins, P. W. (1994). 物理化学 (第4版)。オックスフォード:オックスフォード大学出版局。 ISBN 0-19-269042-6.
- レイドラー、K.J.; Meiser、J.L. (1982)。 物理化学 .ベンジャミン/カミングス。 ISBN 978-0618123414.
- マッカリー、ドナルド。ら。 (2011)。 「解の集合的性質」。 一般化学 .大学科学図書。 ISBN 978-1-89138-960-3.
- Tro, Nivaldo J. (2018). 化学:構造と性質 (第 2 版)。ピアソン教育。 ISBN 978-0-134-52822-9。