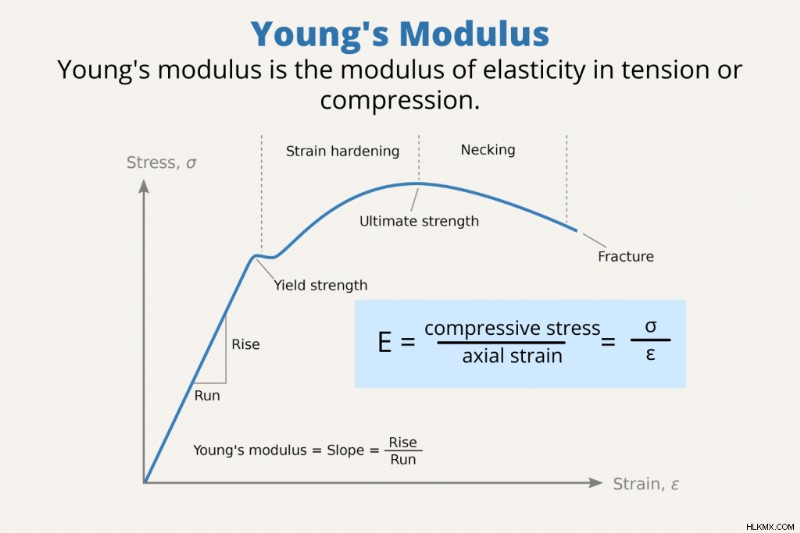
ヤング率 (E ) は、引張りまたは圧縮下の弾性係数です。つまり、素材の硬さ、または曲がりや伸びのしやすさを表します。ヤング率は、応力 (単位面積あたりの力) を軸または線に沿った歪み (比例変形) に関連付けます。
基本的な原理は、材料が圧縮または伸張されると弾性変形し、荷重を取り除くと元の形状に戻ることです。硬い素材と比較して、柔軟な素材ではより多くの変形が発生します。
- ヤング率の値が低いということは、固体が弾性であることを意味します。
- ヤング率の値が高いということは、固体が非弾性または硬いことを意味します。
輪ゴムの挙動は、ヤング率を示しています。輪ゴムは伸びますが、力を離すと元の形に戻り、変形しません。ただし、輪ゴムを強く引っ張ると変形し、最終的には輪ゴムが切れます。
ヤング率の公式
ヤング率は、引張応力または圧縮応力を軸方向ひずみと比較します。ヤング率の式は次のとおりです。
E =σ / ε =(F/A) / (ΔL/L0 ) =FL<サブ>0 / AΔL =mgL0 / π rΔL
場所:
- E はヤング率
- σ は一軸応力 (引張りまたは圧縮) で、断面積あたりの力です
- ε は歪みで、元の長さに対する長さの変化です
- F は圧縮または伸張の力
- A は断面積または加えられた力に垂直な断面
- ΔL は長さの変化です (圧縮時は負、伸張時は正)
- L0 元の長さです
- g は重力による加速度
- r は円柱ワイヤの半径
ヤング率の単位
ヤング率の SI 単位はパスカル (Pa) です。ただし、パスカルは圧力の小さな単位であるため、メガパスカル (MPa) とギガパスカル (GPa) がより一般的です。他の単位には、1 平方メートルあたりのニュートン (N/m)、1 平方ミリメートルあたりのニュートン (N/mm)、1 平方ミリメートルあたりのキロニュートン (kN/mm)、1 平方インチあたりのポンド (PSI)、1 平方インチあたりのメガ ポンド (Mpsi) があります。
問題例
たとえば、長さ 2 m、直径 2 mm のワイヤを 8 kg の質量で引っ張ったときに長さが 0.24 mm 増加した場合のヤング率を求めます。 g を 9.8 m/s と仮定します。
まず、知っていることを書き留めてください:
- 長さ =2 メートル
- Δ L =0.24 mm =0.00024 m
- r =直径/2 =2 mm/2 =1 mm =0.001 m
- m =8 kg
- g =9.8 m/s
情報に基づいて、問題を解決するための最適な公式を知ることができます。
E =mgL0 / π rΔL =8 x 9.8 x 2 / 3.142 x (0.001) x 0.00024 =2.08 x 10 N/m
歴史
その名前にもかかわらず、Thomas Young はヤング率を最初に記述した人物ではありません。スイスの科学者でエンジニアのレオンハルト・オイラーは、1727 年に弾性率の原理を概説しました。1782 年には、イタリアの科学者ジョルダーノ・リカティの実験が弾性率の計算につながりました。英国の科学者トーマス・ヤングは、自然哲学と機械芸術に関する講義で弾性率とその計算について説明しました。 1807年。
等方性および異方性材料
ヤング率は、多くの場合、材料の配向に依存します。ヤング率は、等方性材料の方向に依存しません。例としては、純金属 (特定の条件下で) やセラミックスなどがあります。材料を加工したり、不純物を加えたりすると、機械的特性に方向性を持たせる粒子構造が形成されます。これらの異方性材料は、力が粒子に沿って負荷されるか、粒子に垂直に負荷されるかによって、ヤング率の値が異なります。異方性材料の良い例には、木材、鉄筋コンクリート、炭素繊維などがあります。
ヤング率値の表
この表には、さまざまな材料の代表的なヤング率の値が含まれています。値はテスト方法に依存することに注意してください。一般に、ほとんどの合成繊維はヤング率の値が低くなっています。天然繊維は合成繊維よりも硬いです。金属や合金は通常、ヤング率の値が高くなります。ヤング率が最も高いのは、炭素の同素体であるカルビンです。
| 素材 | GPa | Mpsi |
|---|---|---|
| ゴム(小ひずみ) | 0.01–0.1 | 1.45–14.5×10 |
| 低密度ポリエチレン | 0.11–0.86 | 1.6–6.5×10 |
| 珪藻殻 (ケイ酸) | 0.35–2.77 | 0.05–0.4 |
| PTFE (テフロン) | 0.5 | 0.075 |
| HDPE | 0.8 | 0.116 |
| バクテリオファージ キャプシド | 1–3 | 0.15–0.435 |
| ポリプロピレン | 1.5–2 | 0.22–0.29 |
| ポリカーボネート | 2–2.4 | 0.29-0.36 |
| ポリエチレンテレフタレート (PET) | 2–2.7 | 0.29–0.39 |
| ナイロン | 2–4 | 0.29–0.58 |
| ポリスチレン、固体 | 3–3.5 | 0.44–0.51 |
| ポリスチレン、フォーム | 2.5–7×10 | 3.6–10.2×10 |
| 中密度ファイバーボード (MDF) | 4 | 0.58 |
| 木材 (木目に沿って) | 11 | 1.60 |
| 人間の皮質骨 | 14 | 2.03 |
| ガラス強化ポリエステル マトリックス | 17.2 | 2.49 |
| 芳香族ペプチドナノチューブ | 19–27 | 2.76–3.92 |
| 高強度コンクリート | 30 | 4.35 |
| アミノ酸分子結晶 | 21–44 | 3.04–6.38 |
| 炭素繊維強化プラスチック | 30–50 | 4.35–7.25 |
| 麻繊維 | 35 | 5.08 |
| マグネシウム (Mg) | 45 | 6.53 |
| グラス | 50–90 | 7.25–13.1 |
| 亜麻繊維 | 58 | 8.41 |
| アルミニウム (Al) | 69 | 10 |
| マザーオブパールの真珠層 (炭酸カルシウム) | 70 | 10.2 |
| アラミド | 70.5–112.4 | 10.2–16.3 |
| 歯のエナメル質(リン酸カルシウム) | 83 | 12 |
| イラクサ繊維 | 87 | 12.6 |
| ブロンズ | 96–120 | 13.9–17.4 |
| 真鍮 | 100–125 | 14.5–18.1 |
| チタン (Ti) | 110.3 | 16 |
| チタン合金 | 105–120 | 15–17.5 |
| 銅 (Cu) | 117 | 17 |
| 炭素繊維強化プラスチック | 181 | 26.3 |
| シリコン クリスタル | 130–185 | 18.9–26.8 |
| 錬鉄 | 190–210 | 27.6–30.5 |
| スチール (ASTM-A36) | 200 | 29 |
| イットリウム鉄ガーネット (YIG) | 193-200 | 28-29 |
| コバルトクロム (CoCr) | 220–258 | 29 |
| 芳香族ペプチド ナノスフェア | 230–275 | 33.4–40 |
| ベリリウム (Be) | 287 | 41.6 |
| モリブデン (Mo) | 329–330 | 47.7–47.9 |
| タングステン (W) | 400–410 | 58–59 |
| 炭化ケイ素 (SiC) | 450 | 65 |
| タングステン カーバイド (WC) | 450–650 | 65–94 |
| オスミウム (Os) | 525–562 | 76.1–81.5 |
| 単層カーボンナノチューブ | 1,000+ | 150+ |
| グラフェン (C) | 1050 | 152 |
| ダイヤモンド (C) | 1050–1210 | 152–175 |
| カービン (C) | 32100 | 4660 |
弾性係数
ヤング率の別名は弾性率です 、しかしそれは弾性の唯一の尺度または係数ではありません:
- ヤング率は、反対の力が加えられたときの線に沿った引張弾性率を表します。引張応力と引張ひずみの比率です。
- 体積弾性率 (K) は、ヤング率の 3 次元対応物です。これは、体積応力を体積ひずみで割った値として計算される、体積弾性の尺度です。
- せん断弾性率または剛性係数 (G) は、反対の力が物体に作用するときのせん断を表します。せん断応力をせん断ひずみで割ったものです。
軸弾性率、P 波弾性率、およびラメの最初のパラメーターは、他の弾性率です。ポアソン比を使用して、横方向の収縮ひずみと縦方向の伸長ひずみを比較できます。フックの法則とともに、これらの値は素材の弾性特性を表します。
参考文献
- ASTM インターナショナル (2017)。 「ヤング率、タンジェント弾性率、コード弾性率の標準試験方法」. ASTM E111-17。 Book of Standards Volume:03.01.
- Jastrzebski, D. (1959)。 エンジニアリング材料の性質と特性 (ワイリーインターナショナル編)。ジョン ワイリー &サンズ社
- 劉明傑; Artyukhov、ヴァシリイ I.;リー・フンギョン;徐、方波;ヤコブソン、ボリス I. (2013)。 「第一原理からのカービン:C原子の鎖、ナノロッドまたはナノロープ?」. ACS ナノ . 7 (11):10075–10082。 doi:10.1021/nn404177r
- Riccati, G. (1782). 「Delle vibrazioni sonore dei cilindri」。 めん。マット。フィス。社会イタリア語 . 1:444-525。
- Truesdell、Clifford A. (1960)。 柔軟または弾性体の合理的力学、1638–1788 :Leonhardi Euleri Opera Omnia の紹介、vol. X と XI、Seriei Secundae。オレル・フスリ