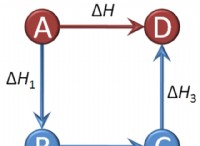
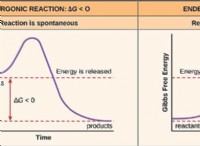
アボガドロの法則のコア コンセプト
この記事では、モルの量が体積にどのように関係するか、およびアボガドロの法則を使用して体積の関係を決定する方法を学びます。
他の記事で取り上げるトピック
- プレッシャーとは
- ダルトンの分圧の法則
- シャルルの法則
- ボイルの法則
- 理想気体の法則
- ファン デル ワールスの状態方程式
- 運動分子理論
- 混合ガス法
考慮すべき重要事項
この記事で説明する気体の法則は、理想気体にのみ適用されます。これについては、The Ideal Gas Law の記事で読むことができます。 .
圧力とモル
1モルの酸素で満たされたピストンを考えてみましょう。ピストンには 1 気圧の圧力がかかります。記事 圧力とは からわかるように 、ガスの圧力はガス粒子と壁との衝突の合計に依存します。
ここで、タンクに酸素をもう 1 モル追加するとどうなるかを考えてみましょう。粒子の量が 2 倍になり、衝突の合計も 2 倍になります。
この 2 倍の量の衝突から、加えられる力は 2 倍になり、したがって圧力も 2 倍になります。ピストンは圧力を均等にするために容積を変化させることができるため、ボイルの法則に従ってピストンが膨張し、容積が増加します。
このことから、モルと体積の関係を見ることができます。
アボガドロの法則の関係
アボガドロの法則はこの関係を説明しており、モルの量と体積は比例すると述べています。これは、次の式で表すことができます。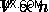 
.
ボイルの法則から、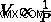 
.この関係から、アボガドロの法則を次のように書き直すことができます。 
.
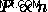一定温度関係
モル数は体積に比例し、容器内のガスのモル数はガスの種類に依存しないため、一定のモル数の体積は特定の温度と温度に対して常に同じです。圧力。
標準条件では、理想気体の場合、この体積は 22.4 L です。これは、1 気圧、摂氏 273 度の気体 1 モルが 22.4 L を占めることを意味します。
アボガドロの法則の例の問題
アボガドロの法則を使用して問題を解決する方法の例を次に示します。
気象観測気球には 25 モルのヘリウム ガスが充填されており、600 L の体積を占めています。気球は膨らみすぎているため、気球を設計している気象エンジニアは、ヘリウム ガスを取り出すことにしました。気象観測気球の標準サイズは 521 L です。気球の体積を安全なサイズに減らすには、何モルのヘリウムを除去する必要がありますか?
解決策:
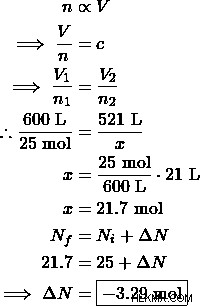
したがって、エンジニアは 3.29 モルのヘリウムガスを取り出す必要があります。
