ボイルの法則のコア コンセプト
このチュートリアルでは、ボイルの法則の公式と、この方程式を使用して特定の閉鎖系における圧力の変化と体積の変化との関係を決定する方法について学習します。
「現代化学の父」と呼ばれることもあるロバート・ボイルは、物理学と化学の分野で活躍しました。 1660 年、ボイルはThe Spring and Weight of the Airを出版しました。 その中で彼は、彼が設計した真空ポンプを使用して作成したさまざまな実験について説明しました.
1662 年、ボイルはThe Spring and Weight of the Airの第 2 版を出版しました。 .これは、現在ボイルの法則として知られている、圧力と体積の逆の関係を彼が説明したものです。ボイルの法則によると、圧力と体積は互いに反比例します。圧力が上がると体積が減り、圧力が下がると体積が増えます。彼は J 管で水銀を使用してこれらの観測を行い、標準大気圧より低い圧力と高い圧力の両方でガスの体積を測定しました。
ボイルは、ボイルの法則の方程式として知られる関係で結果を表現しました またはボイルの法則式:P1 V<小><小>1 =P<小><小>2 V<小><小>2 .この法則は、温度が一定であることを前提としています。
他の記事で取り上げるトピック
- プレッシャーとは
- ダルトンの分圧の法則
- シャルルの法則
- アボガドロの法則
- 理想気体の法則
- ファン デル ワールスの状態方程式
- ゲイ・リュサックの法則
- 混合ガス法
- ヘンリーの法則
考慮すべき重要事項
この記事で説明する気体の法則は、理想気体にのみ適用されます。これについては、The Ideal Gas Law の記事で読むことができます。 .
圧力と体積の関係
1 リットルの容器に入っているガスのサンプルを考えてみましょう。 圧力とはという記事から 、ガスからコンテナに加えられる圧力は、粒子の衝突の合計をコンテナの表面積で割ったものであることがわかっています。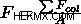 
.また、体積が表面積に関係していることもわかっており、体積が減少すると表面積も減少します。
これらの 2 つの関係から、体積が減少すると、全圧が増加することがわかります。これにより、ボイルの法則の公式が導かれます。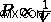 
.
この関係を次のようにグラフ化できます:
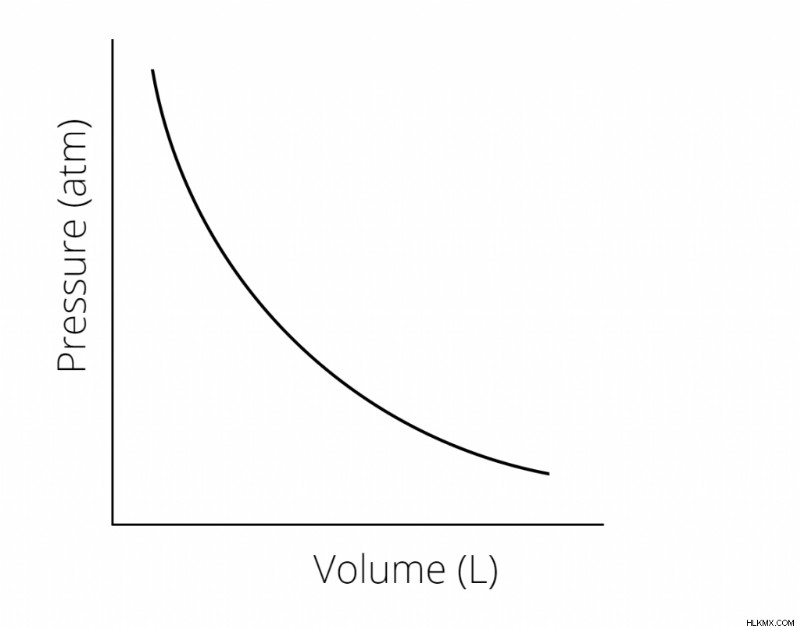
圧力と体積の変化
この比例性により、閉鎖系における圧力と体積の変化に関連する特定の問題を解決することができます。
たとえば、酸素で満たされたピストンを考えてみましょう。この比例関係から、ピストンが圧縮されるとガスの圧力が上昇することがわかります。
ボイルの法則方程式 – 問題例
ボイルの法則の問題を解決する方法の例を次に示します。
理想気体は、2Lの容器で3気圧の圧力がかかります。一定温度で容器の容積を1Lに変化させた場合の圧力は?
解決策:
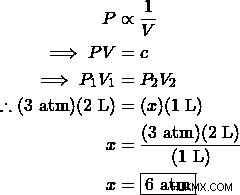
生徒がボイルの元のデータを使用してボイルの法則を検証した方法について読むことができます。
