コア コンセプト
運動分子理論を学びます ガスの平均速度を決定するための二乗平均平方根公式の使用方法。
他の記事でカバー
- ガス圧
- 理想気体の法則
- 状態
運動分子理論 – キーポイント
- すべてのガス粒子は、ランダムな速度でランダムな方向に移動します。
- 粒子が異なる方向に同じ確率で移動している場合、平均速度は 0 になります。
- 速度は方向と大きさの両方を持つベクトルであるのに対し、速度は大きさのみを持つスカラーであることを思い出してください。
- ガス粒子の平均速度は二乗平均平方根の式で計算できます。
基本的な前提
運動分子理論では、ヘリウムのような理想気体の基本的な仮定を使用します。
- 単一のガス粒子が占める体積は、ガス自体が占める体積と比較して無視できます
- ガス粒子は、他のガス粒子に引力または反発力を及ぼしません
また、粒子の運動に関する仮定を立てる必要があります。つまり、
- ガス粒子は動いており、別の物体と衝突するまで一方向にランダムに移動します
- ガス粒子間の衝突は完全に弾性的です
- これは、2 つのガス粒子が衝突すると、衝突中の運動エネルギーが保存されることを意味します
- ガス分子の運動エネルギーは、絶対温度のみに比例します
- これは、温度が絶対零度まで低下すると、粒子の運動エネルギーと速度もゼロまで低下することを意味します。
運動分子理論とは
では、運動分子理論の定義は何ですか?
気体の運動分子理論は、気体サンプル中の粒子のランダムな動きを記述する方法です。個々の粒子はすべて、ランダムな速度でランダムな方向に移動していると述べています。
5 番目の仮定から、このランダムな速度は絶対温度の関数であることを思い出してください。このため、すべての粒子の速度が同じであると想定することができます。ただし、実際にはガスのサンプルにはさまざまな速度があり、温度によって高さと幅が異なる正規分布が形成されます。これらの正規分布をまとめてプロットすると、温度が上昇すると、より高速な粒子の量が増加し、温度が低下すると、より高速な粒子の量が減少することがわかります。
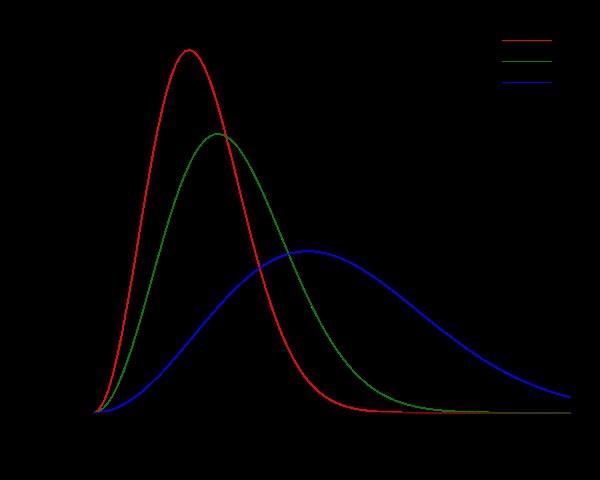
このグラフでは、マクスウェル ボトルツマン分布として知られています 、n 粒子の割合を表し、v 粒子の運動エネルギーを表します。異なる線は、異なる温度での正規分布を摂氏で表しています。
このグラフから、温度が -100 から 600 に上昇するにつれて、より高い運動エネルギーを持つ粒子の量が増加することが明らかです。
平均速度に対する粒子質量の影響
運動エネルギーの方程式を考えてみましょう
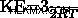
この方程式から、同じ運動エネルギーを持つ粒子の場合、質量が増加すると速度が 2 の累乗で減少することが明らかです。これは、方程式を次の形式に並べ替えることで示すことができます
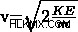
方程式を整理すると、粒子の速度が粒子の質量の逆平方根に比例することが明らかです。
気体の二乗平均速度
温度と質量の両方が気体の平均速度に影響することがわかったので、これらの量を気体の平均速度に関連付ける方程式が必要です。
運動分子理論から、次の式が得られます
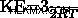
この方程式を、速度を運動エネルギーに関連付ける方程式と組み合わせることで、粒子の質量と温度をその速度に関連付ける方程式を導き出すことができます。
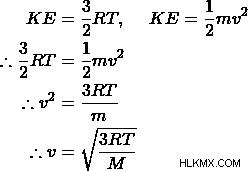
どこで M kg/mol 単位のガスのモル質量、T は温度、R は普遍気体定数です。
この式から、ガスの平均速度を計算できます。
運動分子理論 – 問題例
二乗平均平方根速度とは 摂氏15度のアルゴンガスのサンプルは?
答え:
モル質量 of Ar: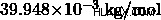
温度 (ケルビン):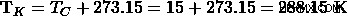
これらの値を二乗平均平方根の式に代入します:

関連記事
- ラザフォードが窒素を発見
- 化学的特性と物理的特性