格子エネルギーとは？

コア コンセプト

このチュートリアルでは格子エネルギーについて 、その定義、関連する周期表の傾向、それに影響を与える要因、および計算方法について説明します.

格子エネルギーとは?

固体イオン化合物の形成中に、電気陽性の金属は電気陰性の非金属と反応します。このような化合物の生成と溶解の両方に、kJ/mol の単位で表されるポテンシャル エネルギーの一種である格子エネルギーの概念が含まれます。格子エネルギーは、イオン化合物内の陽イオンと陰イオンの固定位置を維持します。視点に応じて、この用語を 2 つの異なる方法でさらに調査できます。

この概念を理解する鍵は、イオン性化合物の結晶構造にあります。それらの強力で剛性のある組成により、各荷電イオンと反対の荷電イオンとの間の相互作用が可能になります。これらの相互作用には大量のエネルギーが関与しており、イオン性化合物の高い融点と沸点の特徴を説明しています。

格子エネルギーは、固体イオン化合物 1 モルの形成中にガス状イオンが反応するときに放出される特定量のエネルギーとして説明できます。ただし、1 モルの固体イオン化合物がその構成ガスイオンに解離するのを促進するエネルギーも表します。 選択した定義に応じて、特定のイオン化合物の格子エネルギーは正または負の値になります。

発熱対吸熱

格子エネルギーは、焦点を当てている定義に応じて、吸熱プロセスまたは発熱プロセスのいずれかと見なすことができます。プロセスは、エネルギーを放出するときに発熱します。最初の定義であるイオン化合物の形成には、負の値に対応する発熱格子エネルギーが含まれます。

一方、別の定義、イオン化合物の溶解を使用すると、格子エネルギー値の性質が変化します。このプロセスにはエネルギーが必要なため、正の値に対応する吸熱カテゴリに分類されます。

要因 t 帽子の影響格子エネルギー

1.構成イオンが保持する電荷 (変数 Q₁ で表される) と Q₂ )

イオン電荷変数を増やすと、格子エネルギーが増加します。これは、より大きな電荷値を持つイオンが、より大きな格子エネルギーを持つイオン化合物を生成することを意味します。次に、より弱い電荷を持つイオンは、それらの化合物の格子エネルギーを減少させます。

2.構成イオン間の距離 (変数 R で表される)

距離変数を大きくすると、格子エネルギーが減少します。本質的に、より大きなイオンは、それらの間の距離が増加するため、より小さな格子エネルギーを持つイオン化合物を構成します。小さいイオンは、イオン化合物で大きな格子エネルギーを生成します。

格子エネルギーの傾向

要約すると、イオン電荷が増加し、距離が減少すると、格子エネルギーが増加します。より具体的には、期間全体で左から右に、下から上のグループに増加します。

格子エネルギー周期表の傾向を次の図に要約できます:

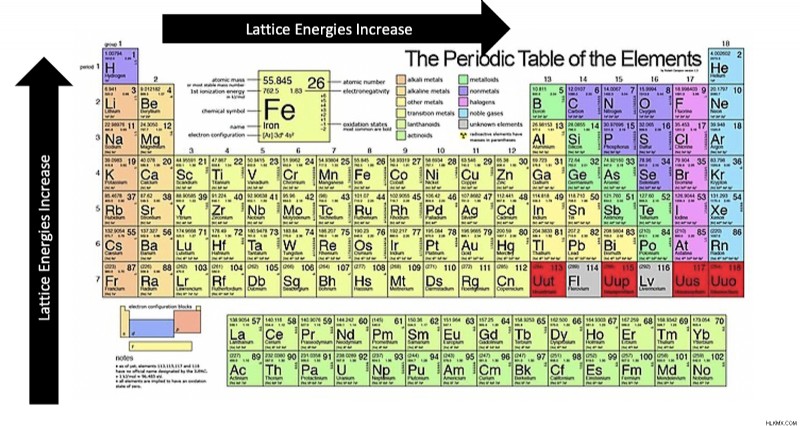
格子エネルギーを見つける

複数のイオン化合物が提示された場合、化学者は多くの場合、どれが最も高い格子エネルギーを示すかを決定しなければなりません。そうするために、彼らはイオン電荷変数と距離変数の両方を考慮します。

格子エネルギーの計算

正確な格子エネルギーの計算は複雑になる可能性がありますが、クーロンの法則を使用してプロセスを単純化することがよくあります。この法則は、特定のイオン化合物の格子エネルギーを表す次の式を提供します:

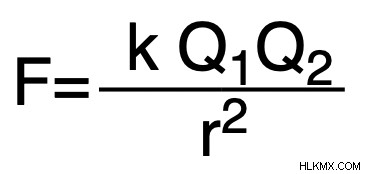
Q₁ &Q₂ =イオン性化合物における構成イオンの相対電荷
R =電荷間の距離
K =2.31 x 10^ J-nm.

最終的な答えは、ジュール (J) の単位で書く必要があります。

解決手順:

格子エネルギーの近似

比較中に、電荷変数と距離変数を使用して、相対的な格子エネルギーを推定することもできます。

解決手順:

1. まず、特定の化合物の各イオンによって示される相対的な電荷を調べます。1 つの化合物のイオン電荷がはるかに高い場合、格子エネルギーが高い可能性があります。

2. 化合物間の電荷の不一致が明確でない場合は、Q₁ を計算します。 x Q₂ 各化合物について、それらの値を比較します。たとえば、-3 の計算された電荷は、-1 の計算された電荷の 3 倍の大きさを持ちます。これは、-3 の電荷を持つイオン性化合物が、-1 の電荷を持つイオン性化合物よりもはるかに高い格子エネルギー (約 3 倍) を示すことを示します。

3. 複数の化合物の電荷が同じか、値が似すぎて区別できない場合は、イオンのサイズを考慮してください。原子サイズを並べて、化合物間の陽イオンと陽イオン、陰イオンと陰イオンを比較します。陽イオン間または陰イオン間でサイズに大きな不一致が見られる場合、原子半径が大きい成分ほど、それぞれの化合物の格子エネルギーが低下します。逆に、原子半径が小さいイオンは、それぞれの化合物のエネルギー値を増加させます。

格子エネルギーの応用

ボーン ハーバー サイクル

格子エネルギーは、化学者が反応エネルギーを分析するのに役立つボルンハーバーサイクルに関与しています。このサイクルは通常、さまざまな元素からのイオン化合物形成の調査に役立ちます。反応プロセス全体を一連のステップに分解して明らかにします。化学反応分析へのこのアプローチは、ヘスの法則に由来します。ヘスの法則は、包括的なエネルギー変化は、個々のステップを調査し、それらの効果を組み合わせることで決定できると述べています。

格子エネルギーはボルン ハーバー サイクルの方程式の一部を形成するため、他の要因が差し込まれている場合はそれを解くことができます。方程式は次のようになります。

生成熱 =格子エネルギー + 原子化熱 + 解離エネルギー + (イオン化エネルギーの合計) + (電子親和力の合計)

Born-Haber Cycle は、ヘスの法則を適用して、特定のイオン化合物の形成エンタルピー変化を、その成分から気体イオンを形成するのに必要なエンタルピーに並置することにより、格子エネルギーを計算します。

格子エネルギーのその他の応用

科学者は格子エネルギーをより広く使用して、電子関係とフッ化物関係を評価します。次に、要因は、さまざまなイオン性固体の相対的な強度に関する調査、およびイオン性化合物のアイデンティティ、成分、および特性に関する予測に役立ちます。

その他の格子エネルギーの計算例

例 s:近似手法の使用

まず、電荷変数を解く練習をします。

問題 1: 化合物 MgO が与えられたら、その複合電荷を決定します。

解決手順:

1. そのイオンの電荷を書き出す:Mgand O

2. これらの料金を掛けます:(2) x (-2) =-4

問題 2: 化合物 KCl が与えられたら、その複合電荷を決定します。

1. そのイオンの電荷を書き出す:Kand Cl

2. これらの料金を掛けます:(1) x (-1) =-1

説明したように、MgO の -4 電荷を KCl の -1 電荷と比較できます。前者は後者の 4 倍の量であるため、その格子エネルギーも約 4 倍になると予測できます。

ここで、サイズ変数を解く練習をします。

問題 3: 化合物 CaO が与えられたら、そのイオンのサイズを決定します。

解決手順:

1. その陽イオンのイオン半径を決定します。Ca のイオン半径は 0.100 nm です。

2. その陰イオンのイオン半径を決定します。O のイオン半径は 0.140 nm です。

説明したように、これらの値を別のイオン化合物の値と比較できます。これにより、どちらがより大きな格子エネルギーを示すかについての洞察が得られます。

ボーン ハーバー サイクル 例

次に、Born-Haber サイクルを使用して正確な格子エネルギーを解く練習をします。

問題 1: 与えられた化合物 NaCl から、その格子エネルギーを決定します。

解決手順:

Na(s)+12Cl₂ (g)→NaCl(s)

2. 反応物をイオンガス成分に変える

Na(s)→Na(g)
Na(g)→Na+(g)+e−

12Cl2(g)→Cl(g)
Cl(g)+e−→Cl−(g)

Na+(g)+Cl−(g)→NaCl(s)

この最終的な変換は、「格子」化合物自体の作成を示しています。

3. ヘスの法則に従って、反応の部分を分離し、それらを分離して考えます。

NaCl(s)→Na(s)+12Cl₂
−ΔH_f,NaCl(s) =+411kJ

Na、Δ=107kJ

Na(g)→Na+(g)+e−
IE_1,Na (g)=502kJ

12Cl₂ (g)→Cl(g)
12ΔH_bond,Cl2 (g)=12×242kJ

Cl(g)+e−→Cl−(g)
EA1,Cl(g)=−355kJ

Na+(g)+Cl−(g)→NaCl(s), ΔH_lattice =?

4. これらのパーツを再結合して、最終的なボルンハーバー サイクル方程式を作成します。

0=ΔHcycle=ΔHf,NaCl(s)+ΔHsub,Na+IE1,Na(g)+12ΔHbond,Cl2(g)−EA1,Cl(g)−ΔHlattice

次に、格子変数を解きます:ΔHlattice,NaCl(s)

=−[411+107+502+12(242)−355]kJ

NaClの格子エネルギー=−786kJ