ギブスの自由エネルギーとは何ですか?|化学

コアコンセプト

ギブスの自由エネルギー は、化学反応の側面を予測できる熱力学の重要な値です。このチュートリアルでは、ギブスの自由エネルギー方程式が重要である理由と、それが関係する問題を解決する方法を学びます。また、自発的な反応とは何かを定義します。

自発的な反応: 温度などの外力がシステムにかかることなく進行する反応
エンタルピー (H): 反応系全体の熱
エントロピー (S): システム内の乱れの量を表す値で、エントロピー値が高いほど乱れが大きくなります。たとえば、固体は秩序のある系 (低エントロピー) と見なされ、液体または気体はより無秩序 (高エントロピー) なシステムと見なされます。
発エルゴン: 反応が自発的な場合
エンダーゴニック: 反応が非自発的な場合

自発的な反応は、生成物の形成に有利な反応です。エネルギーが減少し、エントロピーが増加する反応は自然発生的です。以下に定義する G 値は、反応が自発的かどうかを予測するのに役立ちます。

自発的な反応とは、継続することなく発生する反応であることを覚えておくことが重要です。外部介入またはエネルギーの長期入力。 2H₂ などの自発的な反応 (g) + O₂ (g) -> 2H₂ O(g) が実際に反応を開始するには、火花 (一種の活性化エネルギー) が必要です。

ギブズ自由エネルギー (G) は、反応の自発的性を定義する値であり、負の値は反応が自発的であることを意味し、正の値は反応が非自発的であることを意味します。この値は、エンタルピー (H) とエントロピー (S) の組み合わせです。

ギブスの自由エネルギー、エンタルピー、およびエントロピーはすべて、単純な方程式で関連付けることができます。この式では、G、H、および S は Δ(デルタ) で表され、反応によるこれらの値の変化を示します。式は次のとおりです:

ΔG=ΔH – TΔS

この方程式が成り立つためには、次の 2 つの仮定を行う必要があります:

式に示されている各値が与えられている場合、ギブスの自由エネルギー問題を解くのは簡単です。この反応式から始めましょう:

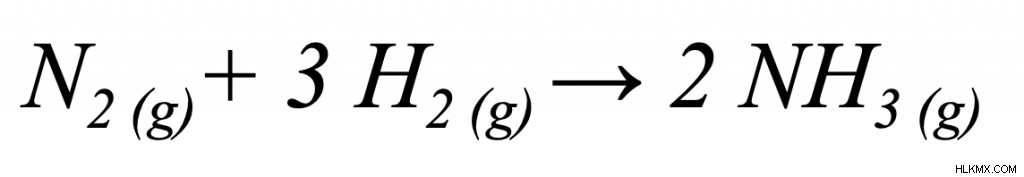
この反応が自発的かどうかを判断できますか?与えられた条件は次のとおりです:

重要: この式が成り立つためには、温度をケルビンに変換する必要があります。摂氏の温度に 273 K を加えてケルビンの値を取得することで、摂氏をケルビンに簡単に変換できます。この場合、273 + 25 =298K です。温度を変換したので、あとはこれらの値を式に代入するだけです!

ΔG=ΔH – TΔS
ΔG= -90 kJ/mol – (298K)(-200 kJ/mol K)
ΔG=-90kJ/mol +59600kJ/mol
ΔG=59510 kJ/mol

ΔG 値が正であるため、この反応は非自発的です。、または エンダーゴニック 反応。

方程式を使用して ΔG を見つける方法がわかったので、ΔG を含むさらに多くの問題を試すことができます。具体的には、ΔG が与えられている場合、方程式内の他の変数のいずれについても解くことができます。次の問題で ΔS を解いてみましょう。

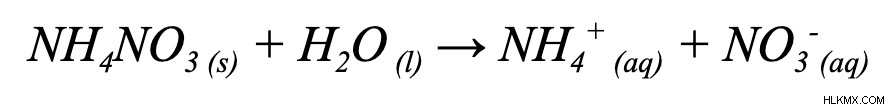
与えられた条件は次のとおりです:

ΔS を解くために式を並べ替えることから始めます。
ΔG=ΔH – TΔS
ΔG + TΔS =ΔH
T∆S=∆H – ∆G
ΔS=(ΔH – ΔG)/T

ΔS を解いたので、値を式に代入できます。最後の問題と同様に、温度をケルビン (この例では 298 K) に変換する必要があります。

ΔS=[28 kJ/mol – (-4.4 kJ/mol)]/298 K
ΔS=32.4kJ/mol/298K
ΔS=0.11 kJ/mol K=110 J/ mol K