主な違い - 定常状態と非定常状態の拡散
絶対零度以外の温度では、物質 (気体、液体、または固体) のすべての原子が常に動いています。これらの動きは互いに衝突を引き起こします。これらの衝突により、粒子の動きはジグザグに見えます。ただし、高濃度の粒子は、拡散として知られる濃度勾配を越えて低濃度に向かって移動する傾向があることが観察できます。拡散は、定常拡散と非定常拡散の 2 種類に分けることができます。定常状態の拡散と非定常状態の拡散の主な違いは、定常状態の拡散は一定の速度で発生するのに対し、非定常状態の拡散の速度は時間の関数であることです。 これらのタイプは両方とも、フィックの法則によって定量的に説明できます。
対象となる主な分野
1.定常状態拡散とは
– 定義、フィックの第一法則との関係
2.非定常状態拡散とは
– 定義、フィックの第一法則と第二法則との関係
3.定常状態と非定常状態の拡散の違いは何ですか
– 主な相違点の比較
重要な用語:衝突、拡散、フィックの法則、定常状態拡散、非定常状態拡散

定常拡散とは
定常状態の拡散は、一定の割合で発生する拡散の一形態です。ここで、特定の界面を横切る粒子のモル数は、時間とともに一定です。したがって、システム全体で、距離による濃度の変化率 (dc/dx) は一定値であり、時間による濃度の変化はゼロ (dc/dt) です。
定常状態の場合、
dc/dx =定数
dc/dt =0
dc は濃度の変化、dx は短い距離、dt は短い時間です。
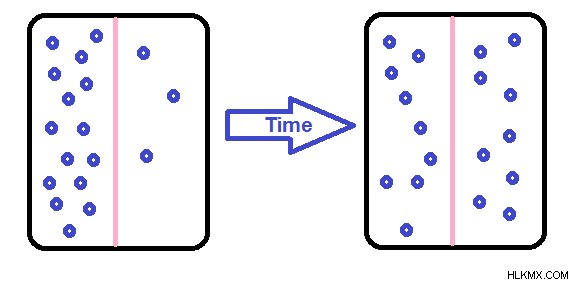
図 1:拡散
フィックの第一法則 定常状態の拡散と非定常状態の拡散の両方を定量的に決定します。フィックの第一法則は、拡散フラックスが既存の濃度勾配に正比例し、数学的に次のように与えられると述べています。
J =-D (dϕ/dx)
その中で、
- J は拡散フラックスです。その次元は、単位時間あたりの単位面積あたりの物質の量であり、単位は mol ms です。
- D は拡散係数です。拡散率とも呼ばれます。このコンポーネントの次元は単位時間あたりの面積であるため、単位は m/s です。
- ϕ は濃度です。単位は mol/m です。
- x は溶質の位置です。このコンポーネントの寸法は長さです。単位は m です。
非定常拡散とは
非定常状態拡散または非定常状態拡散は、拡散速度が時間の関数である拡散の一形態です。これは、拡散速度が時間に依存することを意味します。したがって、距離に対する濃度の比率 (dc/dx) は一定ではなく、時間に対する濃度の変化はゼロではありません。
非定常状態の場合、
dc/dx =時間とともに変化
dc/dt ≠ 0
dc は濃度の変化、dx は短い距離、dt は短い時間です。
フィックの第 2 法則 非定常状態の拡散を定量的に決定します。フィックの拡散の第 2 法則は、拡散が発生したときに濃度が時間とともにどのように変化するかを予測するために使用されます。以下の偏微分方程式で与えられます。
δϕ/δt =D δϕ/δx
その中で、
- ϕ は濃度 (時間と場所 (x) に依存する次元) です。
- t は時間です (s によって与えられます)
- D は拡散係数です。
- X は位置 (長さの次元で指定) です。
したがって、非定常状態は部分拡散方程式として定式化されます。
定常状態と非定常状態の拡散の違い
定義
定常拡散: 定常状態拡散は、一定の速度で発生する拡散の一形態です。
非定常状態 拡散: 非定常状態拡散または非定常状態拡散は、拡散速度が時間の関数である拡散の一形態です。
拡散率
定常拡散: 定常状態の拡散では、拡散速度は一定です。
非定常状態 拡散: 非定常状態の拡散では、拡散速度は一定ではありません。時間によって異なります。
時間依存
定常拡散: 定常状態の拡散は時間とともに変化しません。
非定常状態 拡散: 非定常状態の拡散は時間の関数です (時間とともに変化します)。
フィックの法則との関係
定常拡散: 定常状態は、フィックの第一法則によって定量的に決定できます。
非定常状態 拡散: 非定常状態の拡散は、フィックの第 1 法則と第 2 法則によって定量的に決定できます。
結論
定常状態の拡散と非定常状態の拡散は、2 種類の拡散です。これらのタイプは両方とも、フィックの法則によって定量的に説明できます。定常状態の拡散と非定常状態の拡散の主な違いは、定常状態の拡散が一定の速度で発生するのに対し、非定常状態の拡散の速度は時間の関数であることです。
参照:
1.「拡散メカニズム」。第5章拡散、こちらから入手可能
2. 「粘弾性(非フィック)拡散」。カナディアン ジャーナル オブ ケミカル エンジニアリング、vol. 83、2005 年 12 月、pp. 913–915。
3. 「マルチフィジックス百科事典」。 COMSOL、ここから入手できます。