結合エネルギーの理解
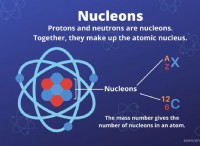
* 核安定性: 原子核は強い核力によって結合され、陽子間の静電反発を克服します。
* 結合エネルギー: この力は、核内の核(陽子と中性子)を完全に分離するために必要なエネルギーである結合エネルギーの原因です。 核子あたりの結合エネルギーが高いと、より安定した核が示されます。
結合エネルギーの計算
1。質量欠陥: 結合エネルギーを計算するための鍵は、質量欠陥の概念にあります。
*核の質量 個々の陽子と中性子の質量の合計よりも *わずかに少ない *。この質量の違いは、質量欠陥と呼ばれます 。
* アインシュタインの有名な方程式(e =mc²) 質量とエネルギーは同等であることを教えてくれます。核が形成されると、質量欠陥はエネルギーに変換されます。
2。方程式:
`` `
結合エネルギー(BE)=(ΔM) *C²
`` `
* Δm 質量欠陥(原子質量単位、AMU)です。
* c 光の速度(299,792,458 m/s)です。
* be 通常、核計算のためにMEV(Megaelectronボルト)で表されます。
ウランの手順(例:ウラン-238)
1。核を識別します: 例として、ウラン-238(²³⁸U)を使用します。
2。陽子と中性子の数を決定します:
*ウランの原子番号(z)は92(陽子)です。
*質量数(a)は238であるため、238-92 =146中性子があります。
3。核の総質量を計算します:
* 92陽子の質量:92 * 1.00728 AMU =92.67296 AMU
* 146中性子の質量:146 * 1.00867 AMU =147.12722 AMU
*陽子と中性子の総質量:92.67296 AMU + 147.12722 AMU =239.80018 AMU
4。質量欠陥(ΔM)を決定:
*ウラン-238の原子質量:238.05078 AMU
*質量欠陥:239.80018 AMU -238.05078 AMU =1.7494 AMU
5。質量欠陥をエネルギー(be)に変換:
* 1 AMU =931.5 MEV/C²
* be =1.7494 amu * 931.5 mev/c²=1632.8 mev
重要なメモ:
* Nucleonあたりの結合エネルギー: これは、異なる核の安定性を比較するためのより便利な尺度です。総結合エネルギーを核子の数で除算します。
* 同位体: ウランにはいくつかのアイソトープ(異なる数の中性子)があり、それぞれがわずかに異なる結合エネルギーを備えています。
ウランの異なる同位体または別の要素の結合エネルギーを計算したい場合はお知らせください!