一定の加速度を伴う直線運動は、加速運動の最も単純な形式です。加速度は一定なので、速度は時間の経過とともに同じ割合で変化します。時間の二乗が進むにつれて位置が変化します。一定の加速度の下での動きを扱うほとんどの宿題の問題を解決するのに役立つ 3 つの基本的な公式があります。
(1) x =x0 + v0 t + ½at
(2) v =v0 +で
(3) v =v0 + 2a(x – x<サブ>0 )
どこ
xは移動距離
x0 最初の出発点です
vは速度です
v0 は初速度
a は加速度
t は時間です
この実用的な問題例は、運動方程式を使用して、一定の速度で移動する別の物体が絶えず加速している物体を横切るのにかかる時間を見つける方法を示しています。
問題例:
時速 120 km で走行しているスピード違反の運転手が、停止しているパトカーを追い越します。パトカーはすぐにスピーダーを追跡し始め、一定の 2.5 m/s で加速します。
(a) パトカーがスピーダーを迎撃するのにどのくらいかかりますか?
(b) パトカーはスピーダーに追いつくまでにどのくらい移動しましたか?
(c) パトカーがスピーダーを横取りしたときの速度はどれくらいでしたか?
解決策:
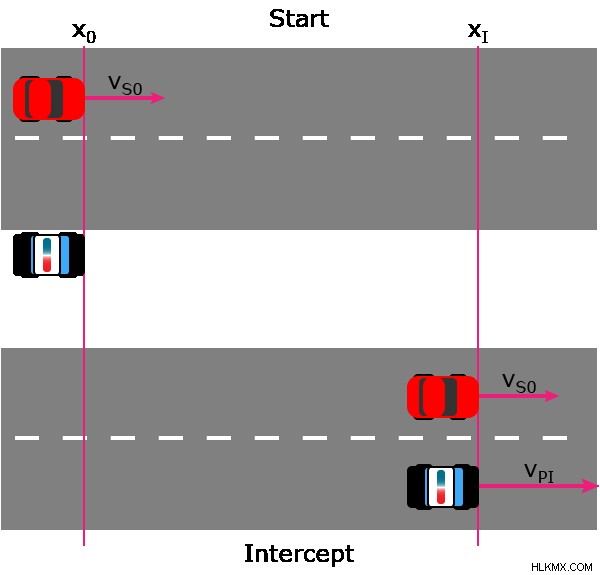
この図は、問題が発生した当初の車両の状態と、パトカーがスピーダーをインターセプトした時点を示しています。
パート a) パトカーがスピーダーを迎撃するのにどのくらいかかりますか?
まず、パトカーの運動方程式を見てみましょう。
xPI =x0P + V0P t + ½at
パトカーは 0 で出発し、停止しているため、v0P =0 その時
xP =½at
vPI =v0P +で
vPI =で
スピーダーの車の運動方程式です。
xS =x0S + V0S t + ½at
x0 =0 で、スピーダーは加速していないため、a =0、したがって
xS =v0S t
vS =v0S +で
vS =V0S
vS =時速120km
加速度は m/s 単位なので、m/s に変換してください。パトカーが追いつくのにおそらく何時間もかからないでしょう。

単位をキャンセルすると、m/s が残ります

掛け算して得る

vS =33.3 メートル/秒
x =0 での追跡の最初の時点では、2 台の車両は同じ位置にありました。どこで再び発生したかを見つける必要があります。これは xPI のときに発生します =xS .
上から:
xPI =½at
xS =v0S t
xPI 以降 =xS 、これら 2 つの方程式を互いに等しく設定できます。
½at =v0S t
この二次方程式には 2 つの解があります。 t の最初の解は t =0 秒です。 2 番目を見つけるには、両辺を t で割ることができます。
½at =v0S
tについて解く

a =2.5 m/s と v0S の値を入力します =33.3 m/s と取得

t =26.6 秒
パトカーがスピーダーに追いつき、迎撃するのに 26.6 秒かかります。
パート b) パトカーはスピーダーに追いつくまでにどのくらい移動しましたか?
時間がわかったので、距離を見つけることができます。上記のパトカーの位置方程式から:
xPI =½at
xPI =½(2.5 m/秒)(26.6)
xPI =888.4 m
パトカーはスピーダーを迎撃するまでに 888.4 m 移動しました。
パート c) パトカーがスピーダーを妨害したときの速度はどれくらいでしたか?
再び、上記の時間とパトカーの速度方程式を使用します:
vPI =で
vPI =(2.5m/秒)(26.6秒)
vPI =66.7 メートル/秒
パトカーはスピーダーを横取りしたとき、速度 66.7 m/s で走行していました。これを時速kmに換算すると、パトカーの速度は時速239.9km。スピード違反の車について話してください。
一定加速度運動の別の例については、運動方程式 - 一定加速度の例の問題を確認してください。この問題は、壊れた車両の位置、速度、および加速度に関する詳細を見つける方法を示しています。