2 つの質量の弾性衝突 – 演習で示すことができます

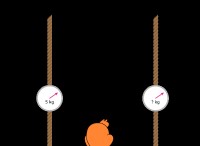
弾性衝突は、総運動量と総運動エネルギーが保存される衝突です。

この図は、2 つのオブジェクト A と B が互いに向かって移動していることを示しています。 A の質量は m_A そして速度 V_Ai で動く . 2 番目のオブジェクトの質量は m_B です 速度 V_Bi . 2 つのオブジェクトが弾性的に衝突します。質量 A は速度 V_Af で遠ざかります 質量 B の最終速度は V_Bf です .

これらの条件を考えると、教科書は V_Af に対して次の式を与えます と V_Bf .

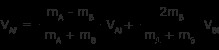
と

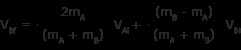
どこ
m_A は最初のオブジェクトの質量です
V_あい は最初のオブジェクトの初期速度です
V_Af は最初のオブジェクトの最終速度です
m_B は 2 番目のオブジェクトの質量です
V_Bi は 2 番目のオブジェクトの初期速度であり、
V_Bf は 2 番目のオブジェクトの最終速度です。

これらの 2 つの方程式は、多くの場合、ほとんどまたはまったく説明なしで、この形式で教科書に表示されます。科学教育のごく初期の段階で、数学の 2 つのステップの間に「それは…を示すことができる」というフレーズや、「学生の練習問題として残す」というフレーズに遭遇するでしょう。これはほとんどの場合、「宿題の問題」に変換されます。この「表示できる」例は、弾性衝突後の 2 つの質量の最終速度を見つける方法を示しています。

これは、これら 2 つの方程式を段階的に導出したものです。

まず、全運動量が衝突で保存されることがわかっています。

衝突前の全運動量 =衝突後の全運動量

m_A V_あい + m_B V_Bi =m_A V_Af + m_B V_Bf

この方程式を並べ替えて、同じ質量が互いに同じ側にある

m_A V_あい – m_A V_Af =m_B V_Bf – m_B V_Bi

質量を因数分解

m_A (V_あい – V_Af ) =m_B (V_Bf – V_Bi )

これを式 1 と呼び、すぐに戻ってみましょう。

衝突は弾性的であると言われたので、総運動エネルギーは保存されます。

衝突前の運動エネルギー =回収後の運動エネルギー

½m_A V_あい + ½m_B V_Bi =½m_A V_Af + ½m_B V_Bf

方程式全体に 2 を掛けて、1/2 の因数を取り除きます。

m_A V_あい + m_B V_Bi =m_A V_Af + m_B V_Bf

方程式を並べ替えて、同じ質量が一緒になるようにします。

m_A V_あい – m_A V_Af =m_B V_Bf – m_B V_Bi

共通質量を因数分解

m_A (V_あい – V_Af ) =m_B (V_Bf – V_Bi )

「2 つの正方形の差」の関係 (a – b) =(a + b)(a – b) を使用して、各辺の速度の 2 乗を計算します。

m_A (V_あい + V_Af )(V_あい – V_Af ) =m_B (V_Bf + V_Bi )(V_Bf – V_Bi )

これで、2 つの方程式と 2 つの未知数、V_Af が得られました。 と V_Bf .

この式を前の式 1 (上記の全運動量式) で割ると、

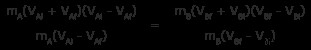
これで、このほとんどを取り消すことができます

これで終了

V_あい + V_Af =V_Bf + V_Bi

V_Af を解く

V_Af =V_Bf + V_Bi – V_あい

これで、他の未知の変数に関して未知数の 1 つが得られました。これを元の全運動量方程式に当てはめます

m_A V_あい + m_B V_Bi =m_A V_Af + m_B V_Bf

m_A V_あい + m_B V_Bi =m_A (V_Bf + V_Bi – V_あい ) + m_B V_Bf

ここで、これを最終的な未知の変数 V_Bf について解きます

m_A V_あい + m_B V_Bi =m_A V_Bf + m_A V_Bi – m_A V_あい + m_B V_Bf

m_A を引く V_Bi 両側から m_A を追加 V_あい 両側に

m_A V_あい + m_B V_Bi – m_A V_Bi + m_A V_あい =m_A V_Bf + m_B V_Bf

2m_A V_あい + m_B V_Bi – m_A V_Bi =m_A V_Bf + m_B V_Bf

質量を因数分解

2m_A V_あい + (m_B – m_A )V_Bi =(m_A + m_B )V_Bf

両辺を (m_A + m_B )

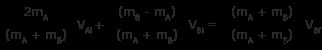
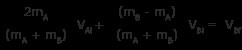
これで、未知数の 1 つである V_Bf の値がわかりました。 .これを使用して、他の未知の変数 V_Af を見つけます。 .以前、見つけました

V_Af =V_Bf + V_Bi – V_あい

V_Bf をプラグインします 式と V_Af の解

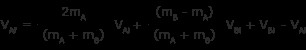
同じ速度の用語をグループ化

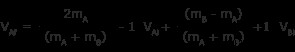
両辺の共通分母は (m_A + m_B )

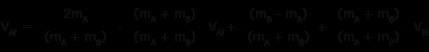
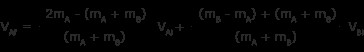
このステップでは、前半の式の記号に注意してください

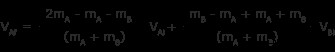
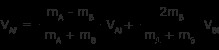
これで両方の未知数 V_Af を解きました と V_Bf 既知の値に関して。

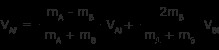
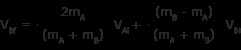
これらは、私たちが見つけるはずだった方程式と一致していることに注意してください。

これは難しい問題ではありませんでしたが、つまずく箇所がいくつかありました。

第一に、手書きを慎重に、またはきれいにしないと、下付き文字がすべてごちゃごちゃになってしまう可能性があります。

次に、エラーに署名します。括弧内の変数のペアを減算すると、両方の変数の符号が変更されます。不用意に – (a + b) を -a – b ではなく -a + b に変えてしまうのはあまりにも簡単です。

最後に、2 つの二乗係数の違いを学びます。 a – b =(a + b)(a – b) は、方程式から何かをキャンセルしようとするときに非常に役立つ因数分解のトリックです。