電場は、荷電粒子が存在する空間内の点に存在する電気的特性として定義できます。電界は、近くに存在する他の荷電物体に力を及ぼします。
加えられる力は、互いに相互作用している電荷の種類に応じて、引力または反発力のいずれかになります。
発射運動は、地球の表面近くに投射され、重力の影響下でのみ湾曲した放物線状の経路を移動する粒子が耐える運動の形態と呼ばれます。
電場と発射体の動きが何であるかを理解したので、次に進み、電場で発射体の動きがどのように発生するかを理解しましょう。
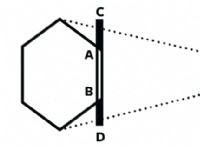
電場 E が空間内で下向きの方向に向けられており、質量 m の荷電粒子が電荷 q を運び、速度 V で移動していると仮定します。ここで、電界に入った後、電荷は下向きの力 F を受けます。
荷電粒子が下向きまたは y 方向 (Fy) に受ける力は qE に等しく、ここで q は粒子の電荷、E は電場です。
電場で発射体運動を受ける荷電粒子の加速の方程式
電場内で発射運動を受ける荷電粒子の加速度には、x 方向と y 方向の 2 つの成分があります。
x 方向の加速度、速度が一定であるため ax=0。
y 方向の加速度 =ay =F/m
上記で、F =qE
に注意しましたしたがって、y 方向の加速度は
ay =qE/m
ここで、q =移動する粒子の電荷
m =移動粒子の質量
E =粒子の電場
電場内で発射運動を受ける荷電粒子の初期速度と移動距離の式
荷電粒子が移動する速度 V には、x 方向の成分と y 方向の成分の 2 つの成分があります。
両方向領域の初速度は次のとおりです:-
x 方向の初速度 (Ux) =V
つまり、速度は x 方向に一定のままです。
y 方向の初速度 (Uy) =0
ここで、荷電粒子が x 方向に移動した距離は次の式で与えられます:-
Sy =ut + ½ a(x)t²
上記で、a(x) =0 と推測しました
したがって、Sx =Vt + ½ at²
荷電粒子が X 空間で x 距離をカバーするとします。つまり、Sx =X
次に、x 方向の距離は X =Vt になります
距離をカバーするのにかかった時間 (X) :-
t =X/V
ここで、荷電粒子が y 方向に移動する距離は次の式で与えられます:-
Sy =ut + ½ ayt²
y 方向の速度 =0、y 方向の加速度 ay =qE/m
したがって、Sy =½ayt²
荷電粒子が Y 空間の距離をカバーするとします。つまり、Sy =y
次に、y 方向の距離は y =½ qet²/m になります
上記では、荷電粒子が距離 (X) をカバーするのにかかる時間を取得しました。- t =X/V
これを置き換えると、y 方向の距離は y =½qe(x²/V²) / m
になります。電場で発射体運動を受ける荷電粒子の最終速度の方程式
荷電粒子の x 方向と y 方向の最終速度は、それぞれ Vx と Vy で表されます。それらの方程式は次のとおりです:-
x 方向の最終速度の式、Vx =Ux + axt
ここで、Ux =V であり、
斧 =0
したがって、x 方向の最終速度
Vx =V
同様に、y 方向の最終速度の式 Vy =Uy + ayt
ここで、Uy =0 であり、
a(y) =qE/m
したがって、y 方向の最終速度、
Vy =qEt/m
上記で、t =X/V
したがって、Vy =qEX/mV
荷電粒子の偏向
荷電粒子の偏向は、荷電粒子が元の経路から偏向する角度として定義されます。これは単純に、x 方向の速度に対する y 方向の速度の比率です。これは tan Θ で表されます。
数式は次のとおりです:-
tan Θ =Vy/Vx
tan Θ =qEX/mV²

X =荷電粒子が X 方向に移動した距離。
m =移動する荷電粒子の質量
V =X 方向の移動粒子の速度
結論
発射体軌道内を移動する荷電粒子のさまざまな運動パラメータは、放物線経路内の粒子の運動と同じです。移動する荷電粒子は、下向きの力を受けます。 X 方向の加速度はゼロですが、y 方向では qE/m に等しくなります。速度の x 成分はパス全体で一定のままですが、Y 成分は 0 です。この知識を使用して、さまざまなパラメーターの方程式が導き出されます。