固有ベクトルは、データセットの特定の特徴を表すベクトルです。固有ベクトルを使用して例題を解決し、概念の理解を深めることが重要です。固有ベクトルは物理学と数学において重要であり、自然および工学システムの多くの側面で役割を果たします。物理学では、固有ベクトルは相対性理論、量子力学、統計力学で重要です。それらは、場の量子論でも使用され、粒子と場の特性を記述します。
固有ベクトル:
これらは、線形システムを固有値と固有ベクトルで表す行列です。固有値はシステムの線形方程式の一意の解であり、固有ベクトルは解の方向を表します。
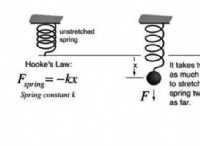
行列 A の固有ベクトルは、次の式によって決定されます:
Av=λv
どこで、
A は線形システムを表す行列です。
v は i 番目の固有値に関連付けられた固有ベクトルです。
λ は v に関連付けられた固有値です。
上記の式は、v が λ 方向の単位ベクトルであることに注意することで簡略化できます。さらに、v はベクトル v をその原点を中心に回転できる回転行列と考えることができます (つまり、Rv =λv、ここで R は回転演算子です)。これが、λ が回転行列の固有値とも呼ばれる理由です。
以下は、概念をよりよく理解するのに役立つ 2 つの例です。
- 例 1:ある企業が、特定の製品を購入する可能性が最も高い顧客を特定したいと考えています。固有ベクトルを使用して、製品の最も重要な機能を表す顧客を見つけることができます。
- 例 2:ある科学者が特定の植物の遺伝子構成を研究しています。彼女は固有ベクトルを使用して、植物の環境によって最も影響を受ける遺伝子を見つけることができます。
マトリックスによる固有値とベクトルの学習
まず、基本的な用語を復習しましょう。
- 行列は、あらゆる種類のデータを表すことができる数値の四角形の配列です。
- 行列の要素は、実数、複素数、ベクトルなど、任意のタイプの数値にすることができます。
- 行列は、行数が列数と等しい正方行列の場合もあります。
- 正方行列は、主対角線より上のすべての要素がゼロであるか、主対角線より下のすべての要素がゼロである三角行列の場合もあります。
固有ベクトルの解決例
<オール>ここで x ≠ 0、x2 =y の解 Ax =b x を解くには 2 つの可能性があります:
- 実数を表す方程式は、本来、線形独立または非結合です。すべてのソリューションのセットは、それらが独立して広がる場合、フィールドと呼ばれるものを形成します。
- x のすべての非負の値に対して ax =b が成立する場合、ベクトル (x)、[x]、…は線形独立です。
1 1 0
0 1 2
0 0 3
この上のマトリックスでは、
<オール>λ2 =1 :v2 =(1, 0, 0).
最終的な一般化された固有ベクトルは、次のような 0 に等しくないベクトル v3 になります。
(A − λ2I)2 v3 =0 ですが、(A − λ2I) v3 は 0 と等しくありません。選択
v3 =(0, 1, 0)。 (A − λ2I)v3 =v2
結論
この記事では、固有ベクトルの解決例について説明します。固有ベクトルは、データ セットの特定の特徴を表すベクトルです。固有値は、システムの線形方程式の一意の解であり、固有ベクトルは解の方向を表します。固有ベクトルを使用して例題を解決し、概念の理解を深めることが重要です。固有ベクトルは物理学と数学において重要であり、自然および工学システムの多くの側面で役割を果たします。物理学では、相対性理論、量子力学、統計力学において固有ベクトルが重要です。