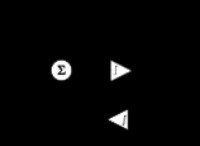
1。ボックスの重量(w) :この力は、重力のために垂直に下方に作用します。
2。通常の力(n) :壁は、壁に垂直な箱に通常の力を発揮し、壁に移動するのを防ぎます。
3。塗布された力(f) :その人は、水平の28度の角度でボックスを上に押し上げています。
ボックスを平衡状態に保つには、水平方向と垂直方向の両方の力の合計がゼロでなければなりません。
水平方向:
$$ \ sum f_x =0 $$
$$ f \ cos28^\ circ -n_x =0 $$
$$ n_x =f \ cos28^\ circ $$
垂直方向:
$$ \ sum f_y =0 $$
$$ f \ sin28^\ circ + n_y -w =0 $$
$$ n_y =w-f \ sin28^\ circ $$
通常の力は壁によって及ぼす反力であるため、正は正しくなければなりません。したがって、$$ n_y $$の方程式から、次のことがわかります。
$$ w> f \ sin28^\ circ $$
これは、ボックスの重量が、壁に対して平衡状態にとどまるために、垂直方向の印加力の成分よりも大きくなければならないことを意味します。
要約すると、28度の角度で適用された力が摩擦力を克服するのに十分であり、ボックスの重量よりも少ない場合、壁は壁に対して所定の位置に残ります。