力を理解する
* 重力の力: この力は常に下方に作用し、物体を地球の中心に向かってまっすぐに引っ張ります。
* 通常の力: この力は、傾斜面の表面に対して垂直に作用し、オブジェクトの重量に押し戻します。
* 摩擦力: この力は動きに反対し、傾斜面の表面に平行に作用します。
* 適用力: これは、オブジェクトを傾斜に移動するために発揮する力です。
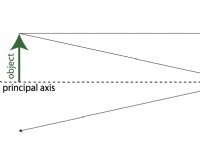
角度の効果:
* より小さな角度:
* 必要な力の少ない: 角度が小さい場合、重力のコンポーネントがオブジェクトを傾斜して引っ張ると小さくなります。 したがって、それを克服してオブジェクトを移動するには、より少ない力が必要です。
* 通常の力の増加: 角度が小さいとは、オブジェクトの重量のより大きな成分が傾斜(正常力)に押し付けられていることを意味します。これにより、摩擦が増加する可能性があります。
* 大きな角度:
* さらに必要な力: 角度が増加すると、傾斜を下回る重力の成分が大きくなります。これは、それに対抗してオブジェクトを移動するために、より多くの力を適用する必要があることを意味します。
* 通常の力の減少: 角度が大きくなると、通常の力が減少します。これは通常、摩擦が少ないことを意味します。
その背後にある数学:
* 重力の成分: オブジェクトを傾斜から引っ張る重力の成分は、次のように計算されます: mg sin(theta) 、 どこ:
* M =オブジェクトの質量
* G =重力による加速(9.8 m/s²)
* theta =傾斜面の角度
* 摩擦力: 摩擦は通常、摩擦係数(μ)に通常の力を掛けたものとして計算されます。通常の力は角度とともに変化します。
キーポイント:
* トレードオフ: 角度が小さくなると、オブジェクトを移動するために必要な力が少なくなりますが、摩擦が増える可能性があります。
* 理想的な角度: 理想的な角度は、オブジェクトの重量、表面、および望ましい速度を考慮して、特定の状況に依存します。
* ゼロ角度: ゼロ度の傾斜は本質的に平らな表面であり、オブジェクトを移動するために最小の力が必要です。
例:
重い箱をランプに押し上げることを想像してみてください。小さな角度のあるランプでは、箱を動かすためにあなたからの力が少なくなりますが、摩擦を克服するために強く押す必要があるかもしれません。急な角度のあるランプでは、ボックスを押すにはより多くの力が必要ですが、摩擦はそれほど問題ではないかもしれません。