軌道角運動量の物理的意義:
l で示される軌道角運動量 、回転オブジェクトの基本的な特性です。それは、特定の軸 *の周りを回転させ続けるオブジェクトの *傾向を説明しています *。 これがその重要性の内訳です:
1。角運動量の保存:
* 重要な原則: 物理学の最も基本的な法則の1つは、角運動量の保存です。これは、閉じたシステムの総角運動量が時間の経過とともに一定のままであることを意味します。
* インパクト: この原則は、オブジェクトが力にどのように回転して応答するかを決定します。たとえば、回転するスケーターは、腕を内側に引っ張り、角運動量を節約することで回転速度を上げることができます。
2。原子物理学の量子化:
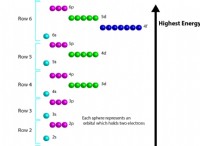
* 電子軌道: 量子の世界では、原子の電子は、惑星が太陽を周回するのと同じように核を周回しません。代わりに、それらの角運動量は量子化されています。つまり、特定の個別の値のみを引き受けることができます。
* 原子スペクトル: この量子化は、原子内の特定のエネルギーレベルにつながります。これは、原子排出量で観察される明確なスペクトル線の原因となります。
3。原子軌道の形状:
* 軌道角運動量と形状: 原子内の電子の軌道角運動量は、その原子軌道の形状を決定します。
* 軌道の種類: 角運動量の異なる値は、S-軌道(球状)、p軌道(ダンベル型)、D軌道(より複雑な形状)などの異なる形状に対応します。
4。磁気モーメント:
* 回転電荷: 移動電荷は磁場を生成します。 これは、軌道角運動量のために軌道電子が磁気モーメントを持っていることを意味します。
* 外部フィールドとの相互作用: この磁気モーメントは、外部磁場と相互作用し、スペクトルラインのZeeman分割のような現象につながる可能性があります。
5。 スピン角運動量:
* 固有の角運動量: 電子は、軌道角運動量に加えて、スピン角運動量と呼ばれる固有の角運動量も持っています。これは量子特性であり、原子の全体的な角運動量に寄与します。
要約: 軌道角運動量は、オブジェクトがどのように回転するか、原子の構造、および磁場での粒子の挙動を説明する重要な概念です。これは、最小の原子から最大の銀河まで、私たちの周りの世界を理解するのに役立つ基本原則です。