それが何を表すかを理解するには、より多くのコンテキストが必要です。
可能な解釈:
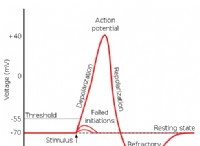
1。 Planckの定数(h)を2π:で割った これは、Planck Constantの減少として知られています(ħ)。これは量子力学の基本定数であり、エネルギーと運動量の量子化を説明するために使用されます。
* 例: 原子のbohrモデルでは、電子の角運動量が量子化され、nは整数であるħ * nによって与えられます。
2。他の定数を2π:で割った 原子構造に関連する他の定数は、特定の計算で2πで分割される場合があります。
* 例: 最初のbohr軌道の半径であるbohr半径は、a0 =ħ^2 /(m_e * e^2 *4πε_0)として表すことができます。ここで、ħはプランク定数が減少し、m_eは電子充電であり、eは初等電荷、ε_0は自由空間の依存率です。
3。周波数/角周波数変換: 場合によっては、定数を2πで割ることは、周波数から角周波数への変換である可能性があります。
* 例: 光子のエネルギーはe =hνで、hはプランクの定数、νは光子の周波数です。これは、e =ħωとして表現することもできます。ここで、ωは角周波数(ω=2πν)です。
より具体的な答えを提供するには、教えてください:
* あなたが言及している特定の定数は何ですか?
* この式が現れる方程式または式のコンテキストは何ですか?
この情報を提供すると、一定のPIが原子理論で示すもので一定の分割を理解するのを手伝うことができます。